Triangle-Ception II
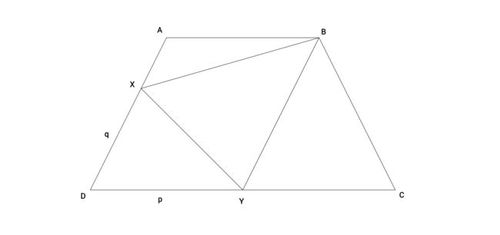 Quadrilateral
A
B
C
D
is an isosceles trapezoid with
A
B
=
6
,
B
C
=
6
,
C
D
=
1
2
,
A
D
=
6
.
Quadrilateral
A
B
C
D
is an isosceles trapezoid with
A
B
=
6
,
B
C
=
6
,
C
D
=
1
2
,
A
D
=
6
.
Points X and Y are chosen on sides A D and D C respectively, such that D X = q and D Y = p .
If the area of triangle X Y B is 1 1 3 , the minimum value of p − q can be expressed in the form m n , where n is not divisible by the square of any prime. Find m + n .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution.
This is exactly my solution, I guess that once one has gotten the enough instinct for problems, the way to go is actually fairly standard
We have four triangles, the central X Y B triangle and the three surrounding triangles, whose area we can find using 2 1 a b sin ( C ) . We can equate the sum to the area of the rectangle: 4 3 [ p q + 6 ( 6 − q ) + 6 ( 1 2 − p ) ] + 1 1 3 = 2 7 3 which simplifies to 6 p + 6 q − p q = 4 4 . ( 1 )
so q (we could equally choose p ) uniquely determines p and therefore p − q . To find the minimum of p − q as q varies, differentiate the above equation (rewritten in terms of ( p − q ) and q ) wrt q and set d q d ( p − q ) = 0 : 6 d q d ( p − q ) + 1 2 − ( p − q ) − d q d ( p − q ) q − 2 q = 0 d q d ( p − q ) = 0 implies p + q = 1 2 . ( 2 )
Together (1) and (2) give us q 2 − 1 2 q + 2 8 = 0 which gives q = 6 ± 2 but it must be 6 − 2 since q ≤ 6 . Keeping in mind that p + q = 1 2 we see that p − q = 4 2 , therefore the answer is 4 + 2 = 6 .
We can figure out the area of the isosceles trapezoid by recognizing that the trapezoid is composed of a rectangle, and two 3 0 o , 6 0 o , 9 0 o triangles. By A r e a = 2 1 ( b 1 + b 2 ) h , we get that the area of the trapezoid is:
2 7 3 .
We can calculate the area of the triangle by taking the area of the trapezoid and subtracting off the area inside of the trapezoid, but outside the triangle. Using SAS area formula , we end up with:
1 1 3 = 2 7 3 − 2 p q sin 6 0 o − 2 ( 1 2 − p ) ( 6 ) sin 6 0 o − 2 ( 6 − q ) ( 6 ) sin 1 2 0 o .
We can manipulate the above equation by multiplying both sides by 3 4 to get:
4 4 = 1 0 8 − p q − ( 1 2 − p ) ( 6 ) − ( 6 − q ) ( 6 ) .
We can expand and move things around to get:
6 4 = p q + 7 2 − 6 p + 3 6 − 6 q .
Using Simon's Favorite Factoring Trick we get:
6 4 = ( 6 − p ) ( 6 − q ) + 7 2 8 = − ( 6 − p ) ( 6 − q ) .
Distribute in the negative for:
8 = ( p − 6 ) ( 6 − q ) .
q and p are real numbers, so for the product to be a positive number, p − 6 and 6 − q must have the same sign. Since 0 ≤ q ≤ 6 due to the side length of the trapezoid, 6 − q can't be negative, so both 6 − q and p − 6 must be positive. This means we can use the AM-GM inequality.
2 6 − q + p − 6 ≥ ( p − 6 ) ( 6 − q ) .
Rearranging once more and substituting 8 for ( p − 6 ) ( 6 − q ) , we get:
p − q ≥ 2 8
p − q ≥ 4 2 .
This means that the minimum of p − q is:
4 2 .
Since 2 is not divisible by the square of any prime, our answer is
4 + 2 + 6 .