TRY from all the ANGLES!!
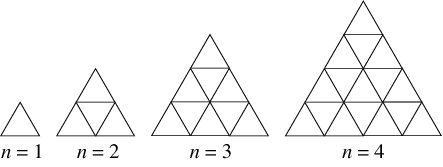 Suppose there is an equilateral triangle with
in the manner shown in the figure above. How many triangles are in that triangle?
Suppose there is an equilateral triangle with
in the manner shown in the figure above. How many triangles are in that triangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The no. of triangles can be obtained by applying any of the two formulas mentioned below:
METHOD 1:
n(∆) =(floor(n x (n+2) x (2n+1))/8)
n(∆) = floor(111 X 113 X 223)/8
n(∆) = floor(2797089)/8
n(∆) = floor(349636.125)
n(∆) = 349636
If you are not familiar with floor function then for your information; floor function in maths is the largest integer less than or equal to the input.
METHOD 2:
If n is even, c n = 8 1 n ( n + 2 ) ( 2 n + 1 ) .
If n is odd, c n = 8 1 [ n ( n + 2 ) ( 2 n + 1 ) − 1 ]