Try it! Just a little geometry

Geometry Level 3

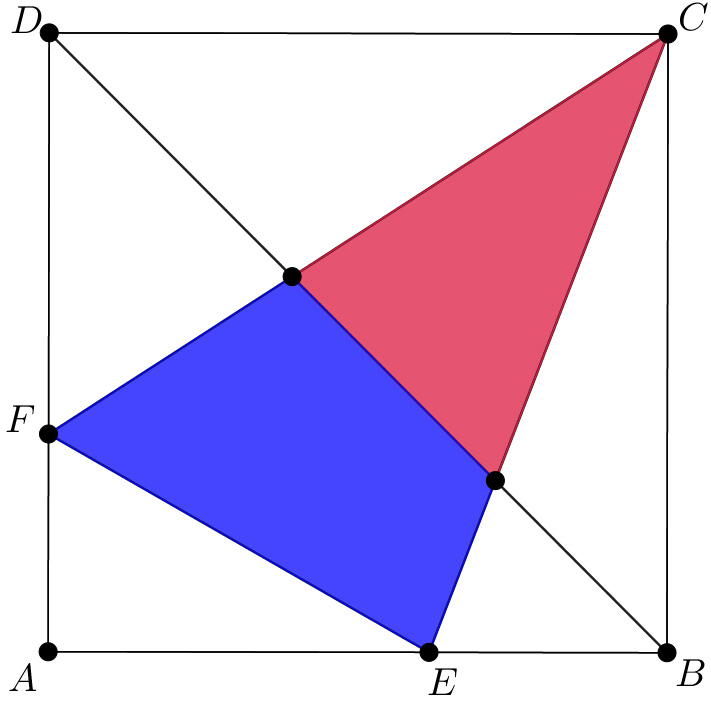
A B C D ABCD is a square which has an area of 1 1 . E E and F F are points on the square's sides as shown in the figure above. Δ A E F \Delta AEF has a perimeter of 2 2 . Diagonal B D BD divides Δ E C F \Delta ECF into two pieces: a smaller triangle and a quadrilateral. Which has a larger area?

They have the same area The blue quadrilateral The red rectangle

Áron Bán-Szabó by Áron Bán-Szabó , 17, Hungary

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

In the next figure the E E and F F points are P P and Q Q . The square was rotated by 90 ° 90° .

If A P = x AP=x and A Q = y AQ=y then P B = 1 − x = P ′ B ′ PB=1-x=P'B' , Q D = 1 − y = Q ′ D ′ QD=1-y=Q'D' and P Q = P ′ Q ′ = 2 − x − y PQ=P'Q'=2-x-y . So P Q ′ = P B + B Q ′ = 1 − x + 1 − y = 2 − x − y PQ'=PB+BQ'=1-x+1-y=2-x-y . Since C Q = C Q ′ CQ=CQ' , the P C Q , P ′ C Q ′ , P C Q ′ PCQ, P'CQ', PCQ' triangles are congurent because they have the same sides. So P C Q ∠ = P C Q ′ ∠ = P ′ C Q ′ ∠ = α PCQ\angle =PCQ'\angle =P'CQ'\angle =\alpha , and Q C D ∠ + P ′ C B ′ ∠ = 90 ° − α QCD\angle+P'CB'\angle=90°-\alpha . Now we get D C B ′ ∠ = 180 ° = 3 ∗ α + ( 90 ° − α ) = 2 α + 90 ° DCB'\angle =180°=3*\alpha+(90°-\alpha)=2\alpha+90° . So α = 45 ° \alpha=45° .

You can find the end of the solution here: Solution part 2

1 Helpful 0 Interesting 0 Brilliant 0 Confused

@aron ban With the configuration provided in the problem you can go for pure sides chasing as well.

Vishwash Kumar ΓΞΩ - 4 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...