Try not to use L'Hôpital!

Calculus Level 3

Find the value of $\displaystyle\lim_{x\to4}\frac{\sqrt[3]{x+4}-\sqrt x}{x-4}$ .

Give your answer to 3 decimal places.

The answer is -0.166666667.

6 solutions

Pi Han Goh
Jul 19, 2015

For the sake of variety, here's an approach that utilize the definition of derivatives.

$\begin{aligned} \displaystyle \lim_{x\to4} \frac{ \sqrt[3]{x+4} - \sqrt x}{x-4} &=& \lim_{x\to4} \frac{ (\sqrt[3]{x+4} - 2 ) - (\sqrt x - 2) }{x-4} \\ &=& \displaystyle \lim_{x\to4} \left( \frac{ \sqrt[3]{x+4} - 2}{x-4} - \frac{\sqrt x-2}{x-4} \right) \\ &=& \left( \frac d{dx} \left. (x+4)^{\frac13} \right |_{x=4} \right) - \displaystyle \lim_{x\to4} \frac{\sqrt x - 2}{(\sqrt x - 2)(\sqrt x + 2) } \\ &=& \left( \left . \frac13 (x+4)^{-\frac23} \right |_{x=4} \right) - \displaystyle \lim_{x\to4} \frac1{\sqrt x + 2 } =\boxed{ -\frac1{6} } \end{aligned}$

Moderator note:

Why didn't you standardize both to doing it via the definition of derivatives?

IE With $f(x) = \sqrt{x}$ , we have $\lim_ { x \rightarrow 4 } \frac{ \sqrt{x} - 2 } { x - 4 } = f' (4)$ .

ChallengeMaster: Oh ahah, yeah I didn't thought of that, I only saw the first one to be applicable. Plus, the second one looks like it's calling out for me to factor it.

Pi Han Goh - 5 years, 10 months ago

Abhay Tiwari
Jul 17, 2015

I did it a bit differently, by taking x as x+h, where h is tending to zero. After that it was a bit easy. After that I opened the binomial expression in the numerator( neglecting the higher terms)

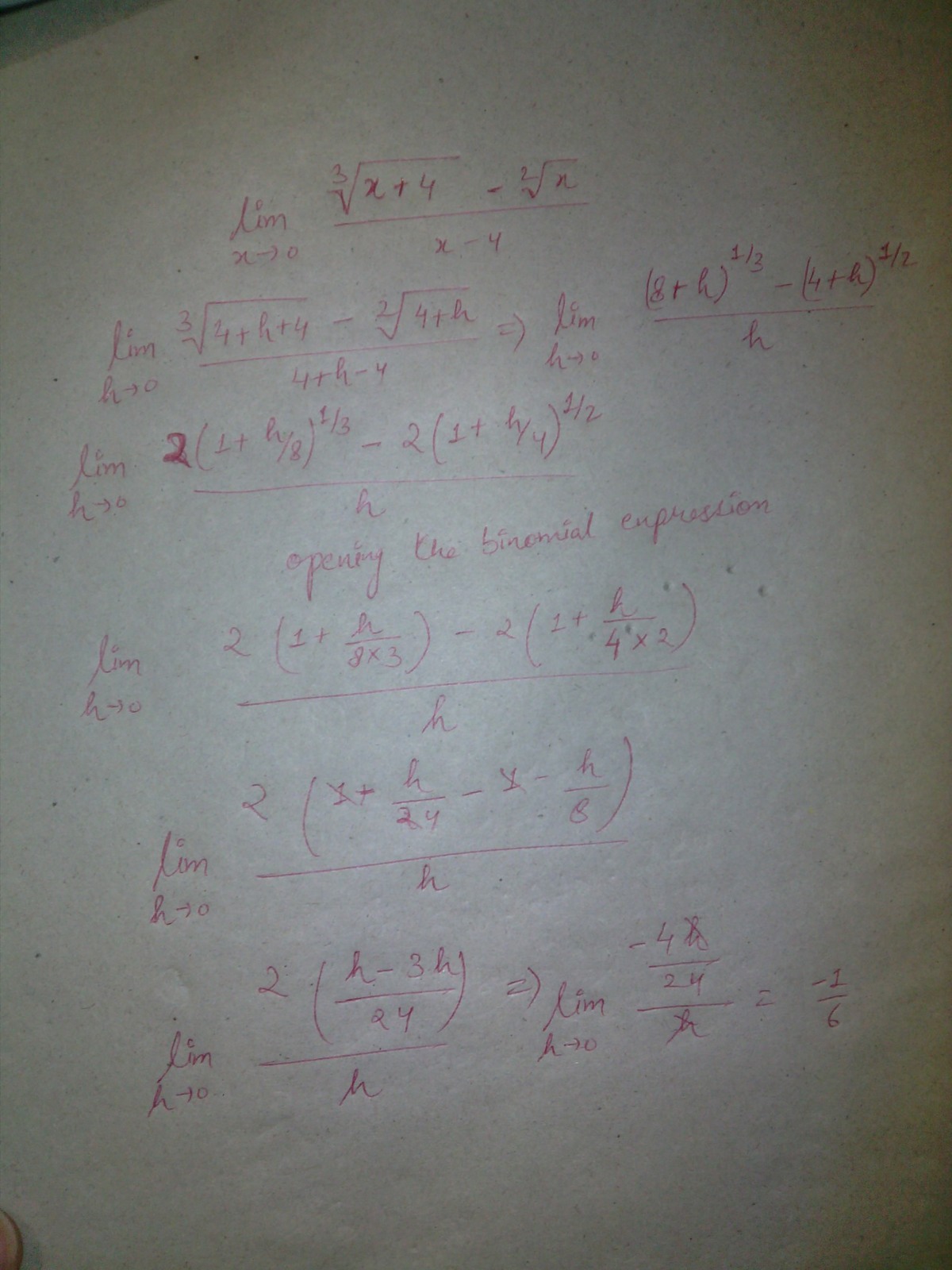
Nice solution! It would be better if you could write $O(h^2)$ and then cancel it with $h$ later to form $O(h)$ . @Isaac Buckley used the same method as you did, so you can refer to his method.

Kenny Lau - 5 years, 11 months ago

Ya thanks. And both of the method are quite similar. I have seen his also.

Abhay Tiwari - 5 years, 10 months ago

Chew-Seong Cheong
Jul 17, 2015

We note that $\displaystyle \lim_{x \to 4} \dfrac{\sqrt[3]{x+4}-\sqrt{x}}{x-4} = \dfrac{g(x) \to 0}{h(x) \to 0}$ . Therefore we can use L'Hôpital's rule.

$\begin{aligned} \lim_{x \to 4} \dfrac{\sqrt[3]{x+4}-\sqrt{x}}{x-4} & = \lim_{x \to 4} \dfrac{g'(x)}{h'(x)} = \lim_{x \to 4} \dfrac{\frac{1}{3}(x+4)^{-\frac{2}{3}}-\frac{1}{2}x^{-\frac{1}{2}}}{1} \\ & = \frac{1}{3}\times \frac{1}{4}-\frac{1}{2}\times \frac{1}{2} = \frac{1}{12} - \frac{1}{4} = - \frac{1}{6} = \boxed{-0.167} \end{aligned}$

Moderator note:

And how about a non-L'hopital approach?

Kenny Lau
Jul 17, 2015

(For worked out solution, scroll down to the second part of this post.)

The technique is to multiply the conjugate until all the roots are gone in the numerator . However, for cube roots, (e.g. $\sqrt[3]a-\sqrt[3]b$ ), instead of multiplying $\sqrt[3]a+\sqrt[3]b$ , we would multiply $\sqrt[3]{a^2}+\sqrt[3]{ab}+\sqrt[3]{b^2}$ to get rid of the cube root.

After multiplying everything and all the roots are gone in the numerator , we would still be expecting a 0/0 form. By the factor theorem, $(x-4)$ would be a factor of the numerator. That is why I created $(x-4)^2$ from $(x+4)^2$ . Then, long division is not needed to factorize the numerator.

If the numerator still cannot be factorized, just use long division.

(For explanation, scroll up to the first part of this post).

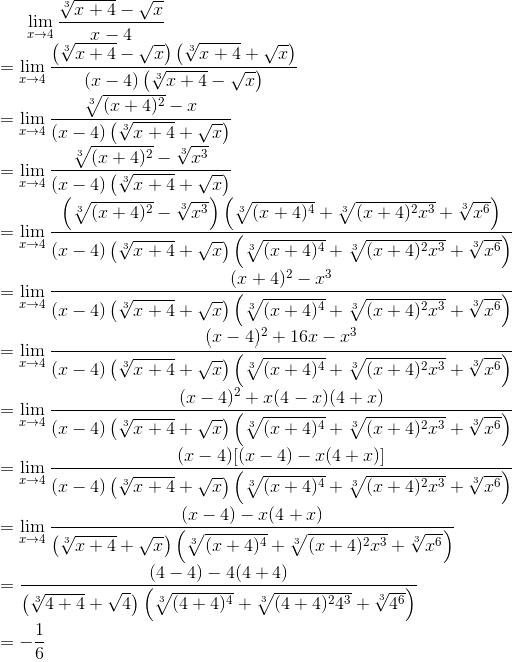
Moderator note:

While you have the correct general idea (and that is indeed what one should do), the act of "multiply by all of the algebraic conjugates" becomes very messy. There is a very simple way to approach this.

Hint: $a - b = \frac{ a^6 - b^6 } { a^5 + a^4 b + a^3 b^2 + a^2 b^3 + ab^4 + b^5 }$

To Challenge Master: I have thought of using that, but I think that fraction is tooooo complicated.

Kenny Lau - 5 years, 11 months ago

Let me demonstrate the "very simple way".

We have $a(x) = \sqrt[3] { x+4} , b(x) = \sqrt{x}$ . $a(4) = b(4) = 2$ . Observe that $a^6 - b^6 = (x+4)^2 - x ^3$ , and so $\frac{ a^6-b^6} { x-4} = -x^2 - 3x - 4$ . We thus get:

$\lim_{x \rightarrow 4 } \frac{ a-b } { x-4} = \lim_{ x \rightarrow 4 } \frac{ a^6 - b^6 } { x-4} \times \frac{ 1} { a^5 + a^4 b + a^3 b^2 + a^2 b^3 + ab^4 + b^ 5 } \\ = ( - 4^2 - 3 \times 4 - 4 ) \times \frac { 1 } { 2^5 \times 6 } = - \frac{1}{6}$

My steps are actually equivalent to yours, because the product of all of the conjugates does lead to the denominator $a^5 + a^4 b + a^3 b^2 + a^2 b^3 + ab^4 + b^ 5$ (I'm not sure if you knew that ). The idea is that we can avoid having to multiply them individually, or figuring out exactly what it looks like.

Calvin Lin Staff - 5 years, 11 months ago

The problem is, the readers might not instantly recognize a sixth power.

Kenny Lau - 5 years, 11 months ago

Isaac Buckley
Jul 17, 2015

$\displaystyle\lim_{x\to4}\frac{\sqrt[3]{x+4}-\sqrt x}{x-4}=\lim_{y\to0}\frac{\sqrt[3]{y+8}-\sqrt {y+4}}{y}\\ =\lim_{y\to0}\frac{2\left(1+\frac{y}{8}\right)^{\frac{1}{3}}-2\left(1+\frac{y}{4}\right)^{\frac{1}{2}}}{y}\\ = \lim_{y\to0}\frac{2\left(1+\frac{y}{24}+o(y^2)\right)-2\left(1+\frac{y}{8}+o(y^2)\right)}{y}\\ =\lim_{y\to0}\frac{-\frac{y}{6}+o(y^2)}{y}=\lim_{y\to0}\left(-\frac{1}{6}+o(y)\right)=- \frac{1}{6}$

Nice solution using taylor series!

Kenny Lau - 5 years, 11 months ago

Devendra Kumar Singh
Sep 15, 2015

Same as that of Isaac Buckley

Try not to use L'Hôpital!

The answer is -0.166666667.

6 solutions

Moderator note:

Moderator note:

Moderator note:

0 pending reports