Try solving this with pure Euclid!
Consider isosceles △ A B C with ∡ A = 2 0 ∘ and A B = A C . Now consider point D on A C such that A D = B C . What is the measure of ∠ B D C ?
(Please don't use trigonometry!)
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
I did exactly this thing
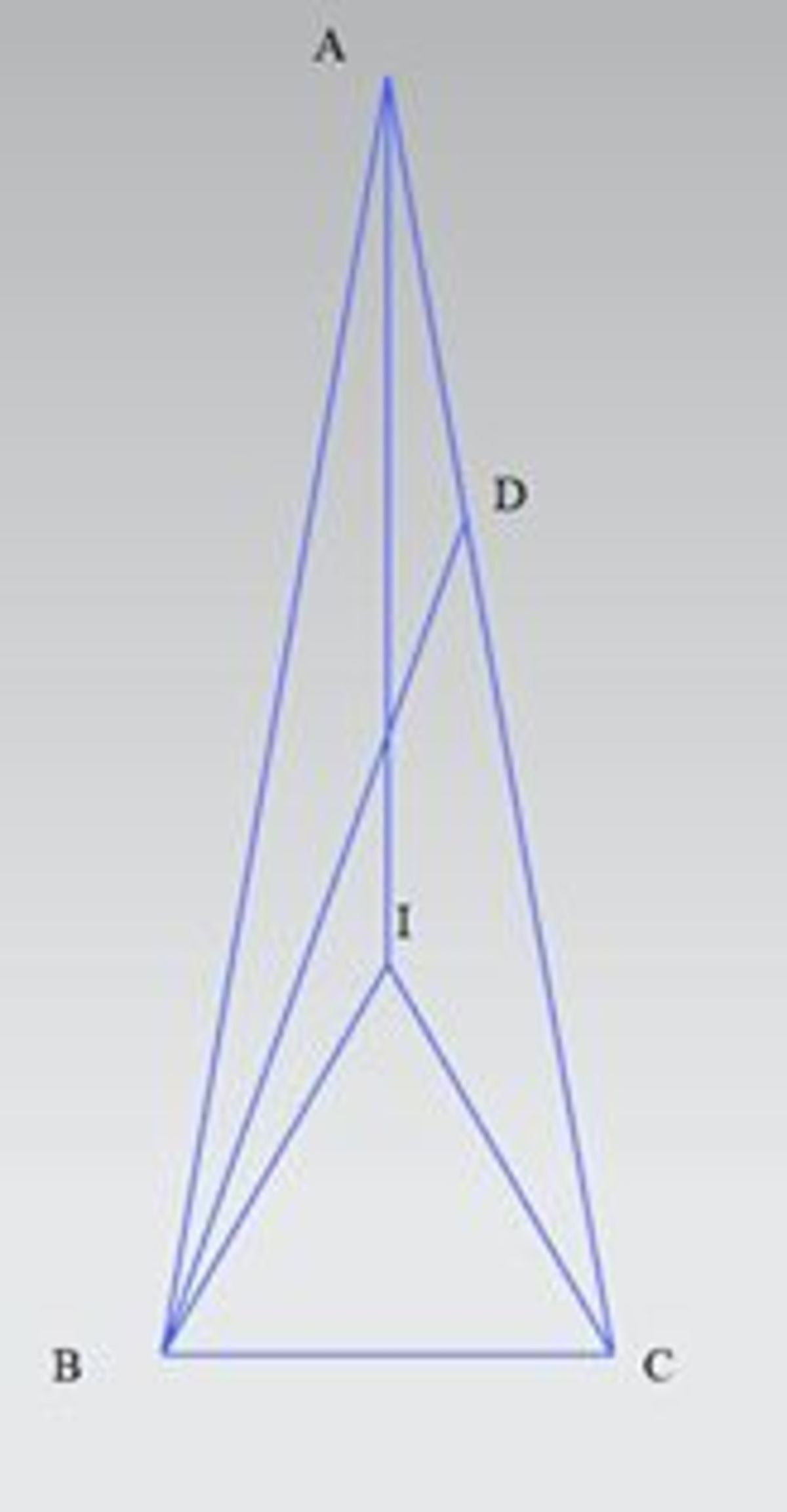 Draw an equilateral triangle inside ABC triangle. BAC=ACI=20, AB=AC, AD=BC=IC => ABD=CAI (s-a-s) => ABD=CAI=10 => BDC=10+20=30
Draw an equilateral triangle inside ABC triangle. BAC=ACI=20, AB=AC, AD=BC=IC => ABD=CAI (s-a-s) => ABD=CAI=10 => BDC=10+20=30
In all Euclidean solutions that are already posted, an equilateral triangle is always the key. So, here is another one:
Let c be the circle with center A and radius A B = R . A C = A B = R , hence, C lies on c . Consider point E on c , such that △ A B E is equilateral and overlapping △ A B C .
∠ B A C = 2 0 ∘ ∠ B A E = 6 0 ∘ } ⇒ ∠ C A E = 4 0 ∘ ⇒ CE ⌢ = 4 0 ∘ ⇒ ∠ C B E = 2 0 ∘
Since B C = A D , B E = A E and ∠ C B E = ∠ B A D , △ C B E = △ B A D (s-a-s), thus, θ = ∠ A B D = ∠ B E C ( 1 )
Alongside, ∠ B A C = 2 0 ∘ ⇒ BC ⌢ = 2 0 ∘ ⇒ ∠ B E C = 1 0 ∘ ⇒ ( 1 ) θ = 1 0 ∘ .
Finally, φ = ∠ B D C = θ + ∠ B A C = 1 0 ∘ + 2 0 ∘ = 3 0 ∘ .
The answer is 3 0 .
W L O G l e t B C = 2 . A B = A C = c o s 8 0 B C D C = A B − B C . D B f r o m D C , D B a n d i n c l u d e d a n g l e C w i t h C o s L a w . U s e S i n L a w i n Δ D B C c a l c u l a t e ∠ C D B . ∴ ∠ C D B = a s i n ⎝ ⎛ 2 2 + ( c o s 2 0 2 ) 2 − 2 ∗ 2 ∗ c o s 2 0 2 ∗ c o s ( 8 0 ) B C ∗ s i n 8 0 ⎠ ⎞ = 3 0 o . I f S i n a n d C o s L a w s a r e a p a r t o f T r i g . , I w i l l p o s t o t h e r s o l u t i o n s o o n .
Not so good. J dim requested not to use trigonmetry.
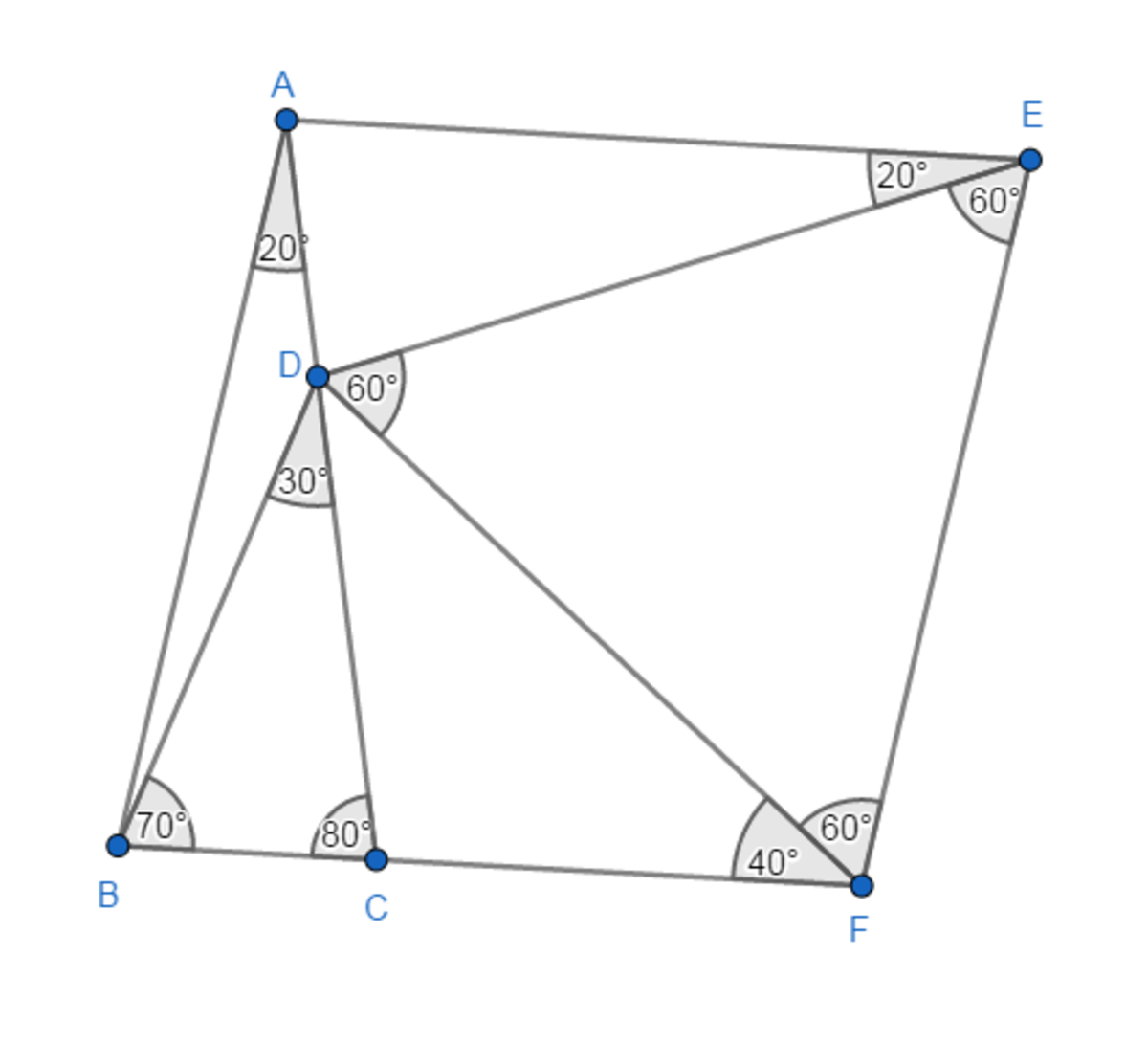
Firstly, ∠ A B C = ∠ A C B = 8 0 °
Now, add a point E , such that △ A B C ≅ △ E A D and △ E A D doesn't overlap △ A B C (i.e. make a copy of △ A B C and position it so that its base completely overlaps segment A D , since A D = B C ). since ∠ A B C + ∠ E A B = ∠ A B C + ∠ E A D + ∠ B A C = 1 8 0 ° , we have that segments B C and A E are parallel. Now, add another point F on line B C such that A B F E is a parallelogram. Not only will A B F E be a parallelogram, but it will be a rhombus as well because A B = A E (from congruency).
Now we have lots of segments of same length:
A B = A C = E A = E D = E F = B F
Because A B F E is a rhombus: ∠ A E F = ∠ A B F = 8 0 ° , so ∠ D E F = ∠ A E F − ∠ A E D = 6 0 ° . With D E = E F and ∠ D E F , we find that △ D E F is equilateral, so we can add D F to the equality above:
A B = A C = E A = E D = E F = B F = D F
Now, since B F = D F , △ B D F is isosceles with ∠ B F D = ∠ B F E − ∠ A F E = 1 0 0 ° − 6 0 ° = 4 0 ° and ∠ D B F = ∠ B D F = 7 0 ° .
In the end, we easily find that ∠ B D C = 1 8 0 ° − ∠ B C D − ∠ D B C = 1 8 0 ° − ∠ B C A − ∠ D B F = 1 8 0 ° − 8 0 ° − 7 0 ° = 3 0 °
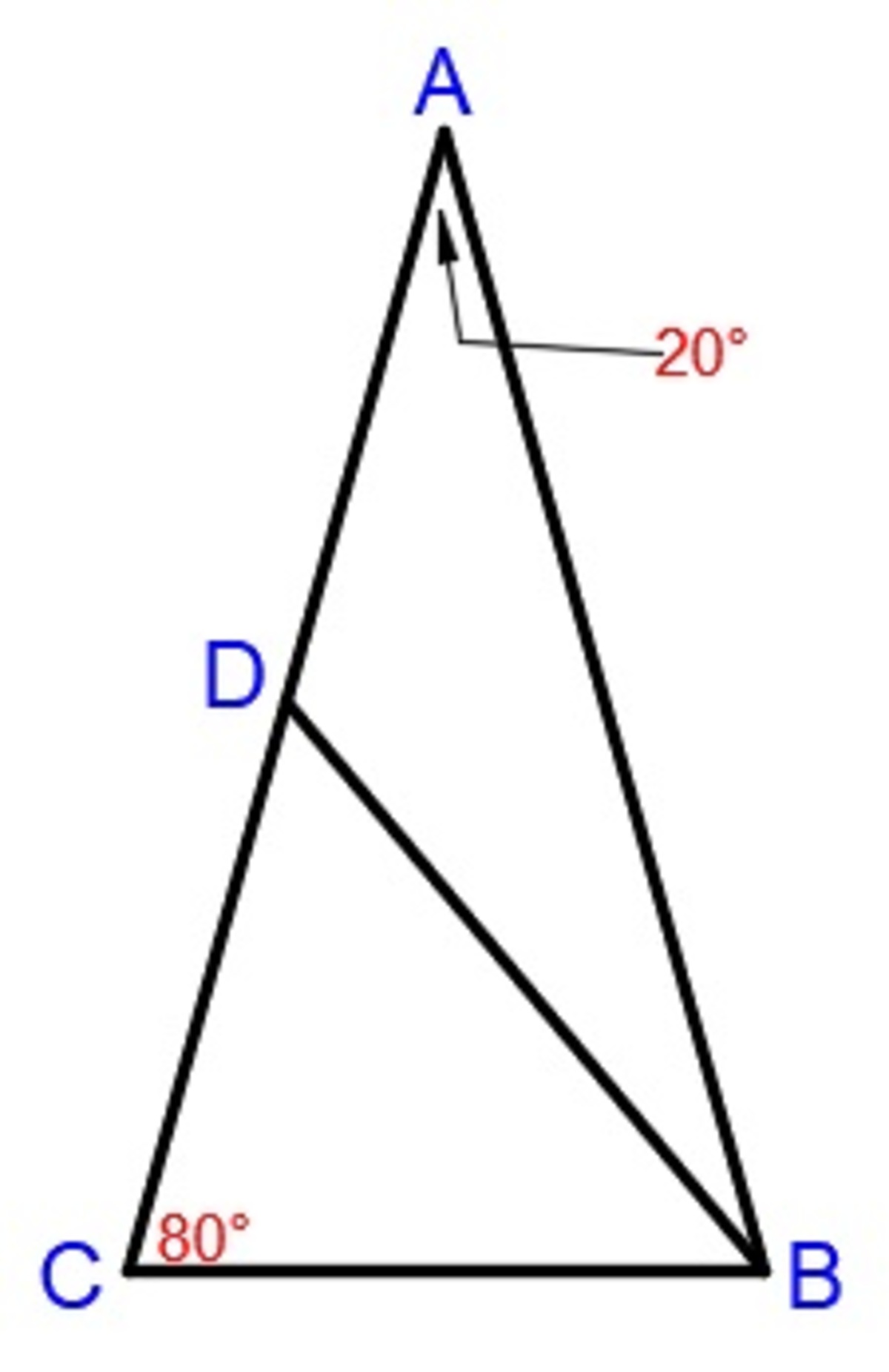 Let
A
B
=
A
C
=
1
. By sine law on
△
A
B
C
,
Let
A
B
=
A
C
=
1
. By sine law on
△
A
B
C
,
sin 2 0 B C = sin 8 0 1 ⟹ B C = sin 8 0 sin 2 0
By cosine law on △ A B D ,
( B D ) 2 = ( sin 8 0 sin 2 0 ) 2 + 1 2 − 2 ( sin 8 0 sin 2 0 ) ( 1 ) ( cos 2 0 )
B D = ( sin 8 0 sin 2 0 ) 2 + 1 − sin 8 0 2 sin 2 0 cos 2 0
By sine law on △ B D C ,
B C sin ∠ B D C = B D sin 8 0
sin 8 0 sin 2 0 sin ∠ B D C = ( sin 8 0 sin 2 0 ) 2 + 1 − sin 8 0 2 sin 2 0 cos 2 0 sin 8 0
∠ B D C = 3 0 ∘
The instruction of the problem is not to directly apply any trigonometric formula.
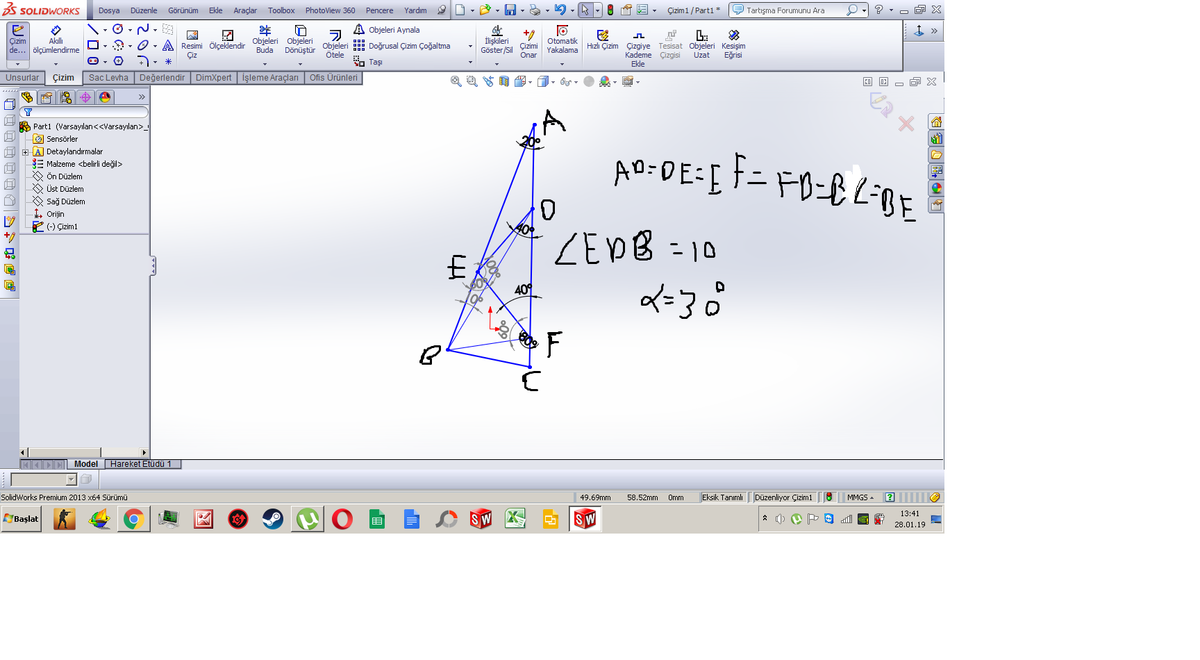
Consider point E such that △ A D E is an equilateral triangle and D E does not intersect with A B . Then △ A B C = △ B E A ( 1 ) . From ( 1 ) we get that △ A D B = △ E D B ( 2 ) . From ( 1 ) and ( 2 ) we get that ∠ A B D = 1 0 ∘ . Thus, ∠ B D C = ∠ A B D + ∠ B A C = 1 0 ∘ + 2 0 ∘ = 3 0 ∘ .