Try the tangent!
Geometry
Level
3
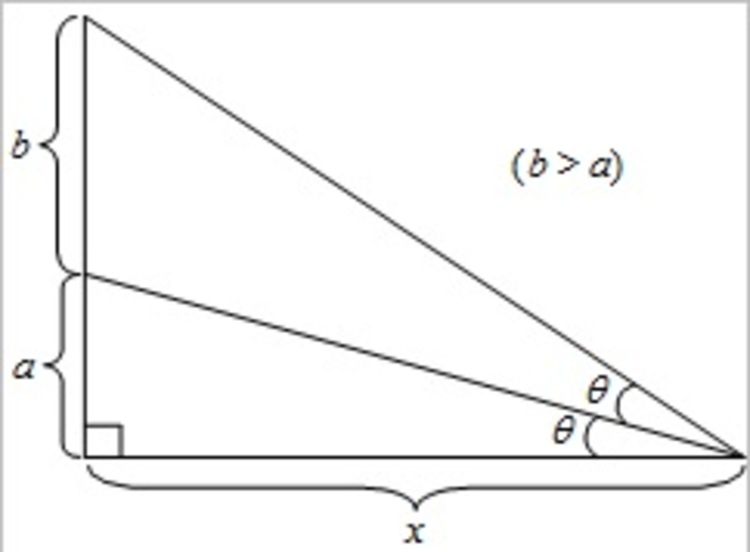A pedestal (height a) sustents a column (height b, b>a). How far from the monument should an observer be so he can see the pedestal and the column under equal angles?
After you find the answer, evaluate it for a=4 and b=5.
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
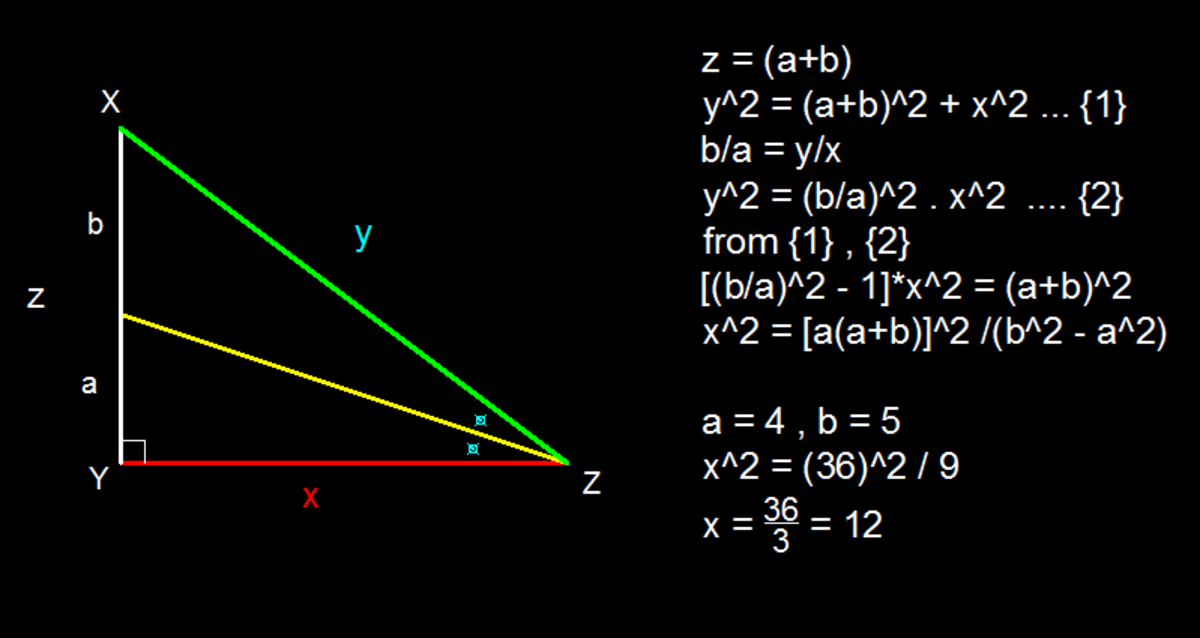
Calculating tangents from the angles:
I) tan(theta) = a/x
II) tan(2theta) = (a+b)/x
2tan(theta)/(1-tan²(theta) = (a+b)/x
(2a/x)/(1 - a²/x²) = (a+b)/x
(2a/x)/[(x²-a²)/x²] = (a+b)/x
2ax²/x[x²-a²] = (a+b)/x
2ax² = (a+b)(x²-a²)
2ax² = (a+b)x² - (a+b)a²
(a+b)x² - 2ax² = (a+b)a²
(b-a)x² = (a+b)a²
x² = a²(a+b)/(b-a)
x = a[(b+a)/(b-a)]^(1/2).
Then, for a=4 and b=5, x = 49^(1/2) = 4*3 = 12.