Try This One on for Size!
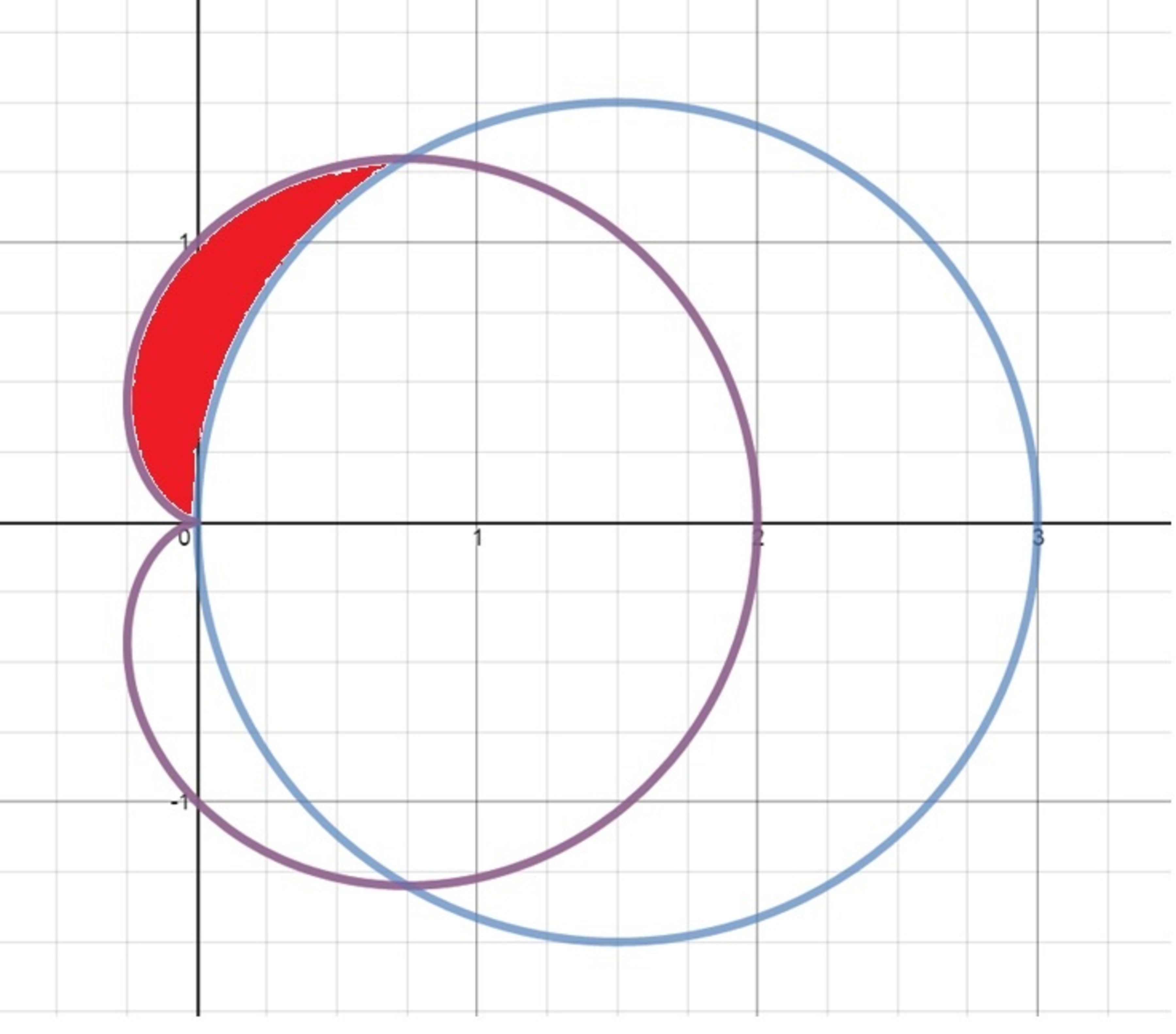
The value of the area shaded in red can be written as
Determine the value of .
The purple curve is a cardioid and the blue curve is a circle .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We first set the curves equal to each other and we see that they intersect at θ = 3 π . Next we need to define our two regions D 1 and D 2 .
D 1 = { ( r , θ ) : 0 ≤ r ≤ 1 + cos θ , 3 π ≤ θ ≤ π }
D 2 = { ( r , θ ) : 0 ≤ r ≤ 3 cos θ , 3 π ≤ θ ≤ 2 π }
And now we need to find the area between the two curves.
Area = 2 [ ∬ D 1 d A − ∬ D 2 d A ]
Being more forthcoming we see
2 [ ∫ π / 3 π ∫ 0 1 + cos θ r d r d θ − ∫ π / 3 π / 2 ∫ 0 2 cos θ r d r d θ ] = 4 π
a = 1 and b = 2 and so 1 × 2 = 2