Try this without calculus (fixed)
A beam of mass and length is supported at each end by two supports A and B. The semicircles and rectangle all have uniform mass densities of . Calculate , where and are the vertical reactions at A and B (in Newtons) respectively. Enter your answer to one decimal place.
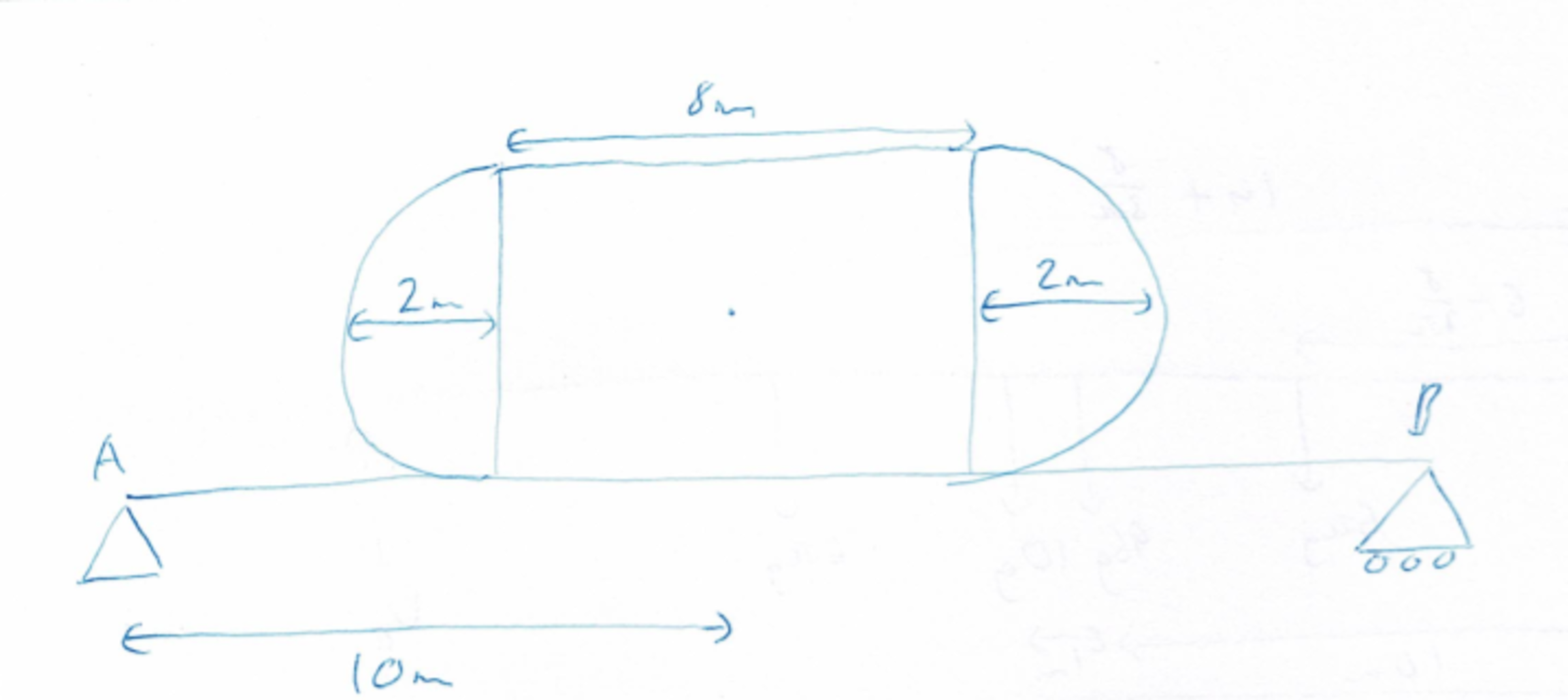
Additional information: (also in diagram)
- The semicircles are identical and each have a radius of .
- The rectangle has a length of .
- The horizontal distance from A to the center of the rectangle is .
- is the gravity constant, .
The answer is 119.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Center of mass of each semicircle is at a distance of 3 π 4 r = 3 π 8 from it's diameter. So, the distances of the centers of mass of the left semicircle, the rectangle, the plank, and the right semicircles are 6 − 3 π 8 , 1 0 , 1 1 and 1 4 + 3 π 8 respectively. Masses of the semicircles and the rectangle are 6 π kg. and 9 6 kg. respectively. Hence, the Force Balance Equation gives
V A + V B = ( 1 0 6 + 1 2 π ) g
Moment Balance Equation about the point A gives
V B × 2 2 = ( 6 π ( 6 − 3 π 8 ) + 9 6 × 1 0 + 1 0 × 1 1 + 6 π ( 1 4 + 3 π 8 ) ) g = ( 1 2 0 π + 1 0 7 0 ) g ⟹ V B = 1 1 5 ( 1 2 π + 1 0 7 ) g ⟹ V A = 1 1 1 ( 7 2 π + 6 3 1 ) g ⟹ V A − V B = 1 1 1 2 ( π + 8 ) g ≈ 1 1 9 . 2 3 5 2 9 8 8 N.