Try your intuition!

Calculus Level 3

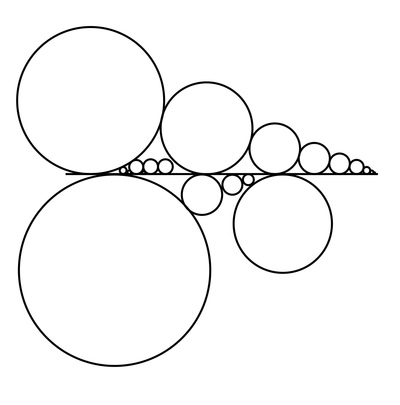
Is it possible to cover the closed line segment $\left[ 0,1 \right]$ with (possibly infinitely many) circles of positive radius such that no circles overlap (they can touch each other) and the circles only touch the line segments?

No Yes

1 solution

Mark Hennings
Oct 24, 2019

Let $\{\mathbf{x}_n\,:\, n \in \mathbb{N}\}$ be an enumeration of the subset $\mathbb{Q}^2$ of $\mathbb{R}^2$ . For any disk $C$ with positive radius, there must be some elements of $\mathbb{Q}^2$ in the interior of $C$ , and so we can define the integer $F(C)$ , where $F(C)$ is the smallest integer $n$ such that $\mathbf{x}_n$ belongs to the interior of $C$ .

If $\mathcal{C}$ is any collection of nonoverlapping disks of positive radius, then the function $F\,:\, \mathcal{C} \to \mathbb{N}$ is injective (distinct elements of $\mathcal{C}$ have disjoint interiors). This means that $\mathcal{C}$ is countable.

Suppose that all elements of $\mathcal{C}$ are tangential to the $x$ -axis, and that every element of the $x$ -axis belongs to at least one element of $\mathcal{C}$ . If we define $G(x)$ to be equal to the least integer $F(C)$ where $C$ is a disk in $\mathcal{C}$ that contains $(x,0)$ (there is always at least one, and no more than two, such disks for any $x \in \mathbb{R}$ ), then $G\,:\, \mathbb{R} \to \mathbb{N}$ is injective (no two elements of the $x$ -axis can belong to the same disk in $\mathcal{C}$ ). This would require $\mathbb{R}$ to be countable, which is not true.

Thus no such collection of disks $\mathcal{C}$ can exist.

Followup question: can you cover every rational point on the line segment?

Simon Kaib - 1 year, 7 months ago

Yes.

Let $\{\mathbf{x}_n = (q_n,0)\,:\, n \in \mathbb{N}\}$ be an enumeration of the rationals on the $x$ -axis. Pick $r_1 > 0$ , and let $C_1$ be the disk with centre $(q_1,r_1)$ and radius $r_1$ .

For any $n \in \mathbb{N}$ , suppose that we have found disjoint circles $C_1,...,C_n$ which touch the $x$ -axis so that $\mathbf{x}_k \in C_k$ for each $1 \le k \le n$ . Then $\mathbf{x}_{n+1}$ lies outside all of $C_1,...,C_n$ , and so we can find $r > 0$ such that the distance from $\mathbf{x}_{n+1}$ to $C_k$ is at least $r$ for all $1 \le k \le n$ . Now set $r_{n+1} = \tfrac12r$ , and let $C_{n+1}$ be the disk with centre $(q_{n+1},r_{n+1})$ and radius $r_{n+1}$ . Then $C_{n+1}$ touches the $x$ -axis at $\mathbf{x}_{n+1}$ and is disjoint from $C_1,...,C_n$ . The result now follows by induction.

Mark Hennings - 1 year, 7 months ago

See Ford Circle .

Jon Haussmann - 1 year, 7 months ago

Is it wrong to think that no matter how small the circles are, there will always be a small amount of gap between them, leaving at least a very small, say $x$ amount of area uncovered. So $x$ may tend to $0$ as the circles get smaller, but it can never be equal to $0$ .

Adhiraj Dutta - 1 year, 1 month ago

This exact argument would only work for a finite amount of circles. If you only consider rational numbers, for example, your argument will still hold but it is actually possible to cover all rational numbers with infinitely many circles.

Simon Kaib - 1 year, 1 month ago

It is quite difficult for me to imagine this, but thank you! Learnt a new thing.

Adhiraj Dutta - 1 year, 1 month ago

Try your intuition!

1 solution

0 pending reports