This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Intelligent,Chew-Seong
Good but very lengthy solutions!
superb.......!!
nice solution
very good.
I've got a solution for the general case. Let us suppose a =2006, (a+1 = 2007). Thus n = a 2 + ( a + 1 ) 2 − 1 Thus 2 n + 1 = 2 ( a 2 + ( a + 1 ) 2 − 1 ) + 1 = 4 a 2 + 4 a + 1 = ( 2 a + 1 ) 2 By applying the sqrt ( 2 n + 1 ) = 2 a + 1 leading us to the solution 4013. Notice that this formula is valid for any real a.
I Came Nearer To It But I Did Not Think in Such a way
i have done this
nice solution
I did the same way
n + 1 = 2 0 0 6 2 + 2 0 0 7 2 ,
n + 1 = 2 0 0 6 2 + ( 2 0 0 6 + 1 ) 2 ,
n + 1 = 2 0 0 6 2 + 2 0 0 6 2 + 1 + 2 . 2 0 0 6 . 1 ,
n = 2 0 0 6 2 + 2 0 0 6 2 + 2 . 2 0 0 6
2 n = 4 . 2 0 0 6 2 + 4 . 2 0 0 6
2 n + 1 = 4 . 2 0 0 6 2 + 4 . 2 0 0 6 + 1
now make perfect square a nd you will get the answer 4 0 1 3
n+1=2006^2+(2006+1)^2 2n=4012^2+2*4012 sqrt(2n+1)=4012+1=4013
: n+1 = 2006^2 + 2007^2
: n+1 = 2006^2 + (2006+1)^2
: n+1 = 2006^2 + 2006^2 + 2 * 2006 + 1
: n+1 = 2 * 2006^2 + 2 * 2006 + 1
: n = 2 * 2006^2 + 2 * 2006
: 2n = 4 * 2006^2 + 4 * 2006
: 2n+1 = 4 * 2006^2 + 4 * 2006 + 1
: 2n+1 = (2 * 2006+1)^2
: sqrt(2n+1) = 2 * 2006+1
Formula using:
x2 + y2 = (x-y)2 + 2
x
y
x2 – y2 = (x+y)(x-y)
Solution :
N + 1 = 20072 +20062
N + 1 = (2007-2006)2 + 2
2007
2006
N +1 = 12 + 2
2007
2006
N = 2
2007
2006
So, √2N +1 = √2
2
2007
2006 +1
√2N +1 = √2
2007
2
2006 +1
√2N +1 = √4014*4012 +1
√2N +1 = √(4013+1)(4013-1) +1
√2N +1 = √40132 -12 + 1
√2N +1 = √40132 -1 + 1
√2N +1 =√40132
√2N +1 = 4013
ea bornok ...
2n + 1 = 2 \times 2006^{2 } + 2 \times 2007^{2} - 1
2n + 1 = 2 \times 2006^{2 } + 2 \times 2007^{2} - (2007 - 2006)^{2}
2n + 1 = 2006^{2 } + 2007^{2} + 2 \ times 2006 \ times 2007
2n + 1 = (2007 + 2006)^{2}
\sqrt{2n +1} = 4013
Let a = 2006 then a² + (a + 1)² = n + 1
2a² + 2a = n
2n + 1 = 2(2a² + 2a) + 1 = 4a² + 4a + 1 = (2a + 1)²
(2n + 1)^1/2 = 2a + 1 = 2006 × 2 + 1 = 4013
Let x=2006
n+1=x^2 + (x+1)^2
n+1=x^2 + x^2 +2x +1
n=2x^2 + 2x
Sqrt (2n +1)=sqrt (4x^2 +4x+1)
=sqrt (2x+1)^2
=2x+1
=2 (2006)+1
=4013
I just rewrote the 1 in LHS as (2007-2006)^2 and expanded. Then, the two terms in the RHS cancel, resulting in n = 2×2006×2007. Later, I calculated the root as sqrt (n+n+1), where I substituted the original equation and and that obtained before. Thus, sqrt (2006^2 + 2007^2 + 2×2006×2007) = sqrt[(2006+2007)^2] = 2006+2007 = 4013. Done!
first, find n. n=(2006 2006) + (2007 2007) -1 n=8,052,084
then sqrt 2(8,052,084) + 1
sqrt 16,104,169
equals 4013
We have, n+1=2006^2 + 2007^2 & by solving we get, n=8052084.. Now put the value of n ... We get 4013 which is the required answer.
Let x = 2006.
2006^2 + 2007^2 = x^2 + (x + 1)^2
n + 1 = x^2 + x^2 + 2x + 1
n = x^2 + x^2 + 2x = 2x^2 + 2x
2n + 1 = 4x^2 + 4x + 1 = (2x + 1)^2
Sqrt(2n + 1) = 2x + 1 = 2×2006 + 1 = 4013
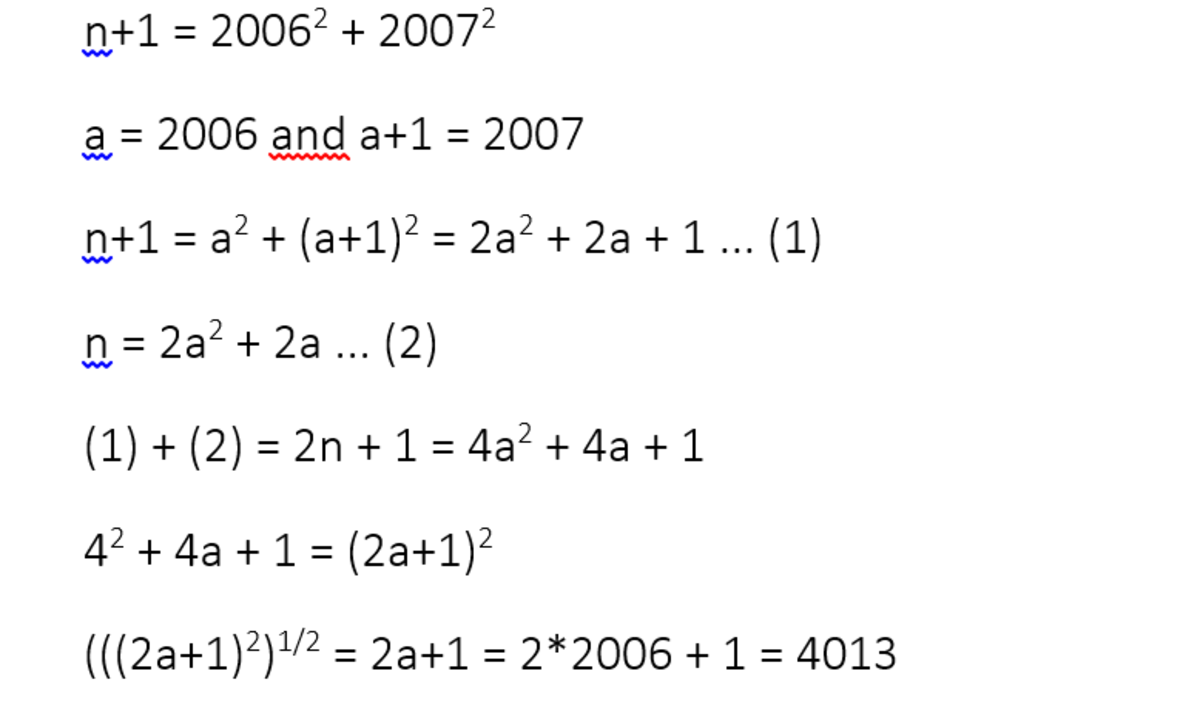
n + 1 = 2 0 0 6 2 + 2 0 0 7 2
⇒ n = 2 0 0 6 2 + 2 0 0 7 2 − 1
= 2 0 0 6 2 + ( 2 0 0 7 + 1 ) ( 2 0 0 7 − 1 )
= 2 0 0 6 2 + 2 0 0 8 ( 2 0 0 6 )
= 2 0 0 6 ( 2 0 0 6 + 2 0 0 8 )
= 2 0 0 6 ( 4 0 1 4 )
⇒ 2 n + 1 = 4 0 1 2 ( 4 0 1 4 ) + 1
= 4 0 1 2 ( 4 0 1 2 + 2 ) + 1
= 4 0 1 2 2 + 2 ( 4 0 1 2 ) + 1
= ( 4 0 1 2 + 1 ) 2 = 4 0 1 3 2
⇒ 2 n + 1 = 4 0 1 3