Tsunami and Volcano Problem

Here’s how you approach it:

-The best way to solve this problem is by looking at the annual probability that neither event happens.

-Since both volcano and flood will create wreak havoc on the property, either event happening is bad.

-Once the probability of not getting hit by a natural disaster in a given year is figured out, then we can figure out how long it’s going to take before you’re pretty sure it’s going to happen.

First figure out the probability of neither event from happening in a given year:

Calculate the annual odds: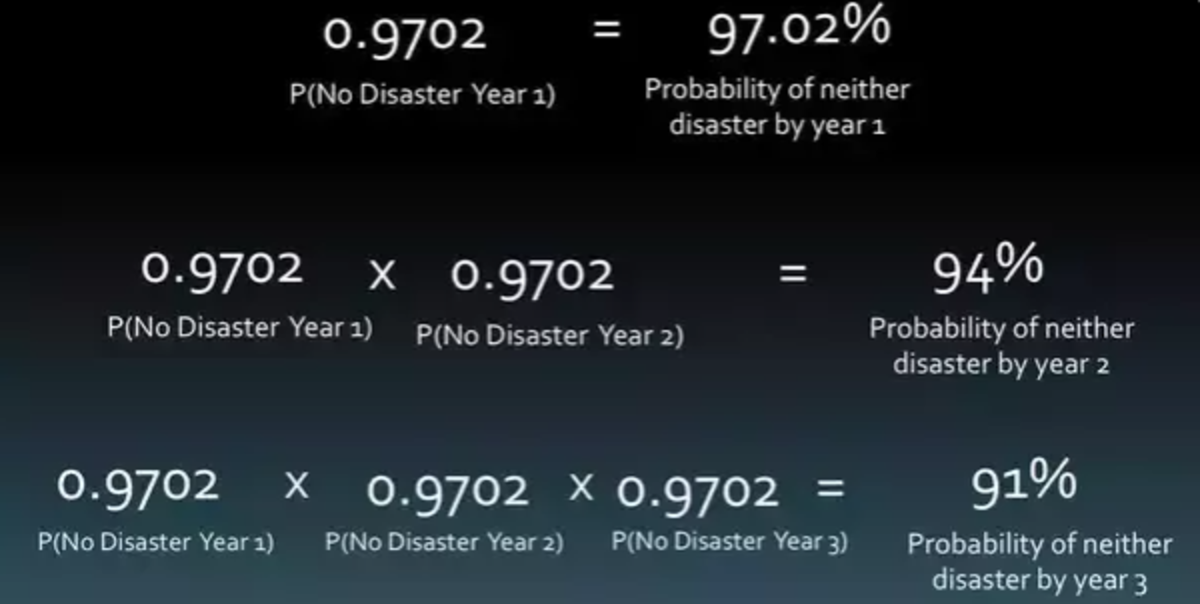

Now extrapolating the values for each new year and each new annual risk: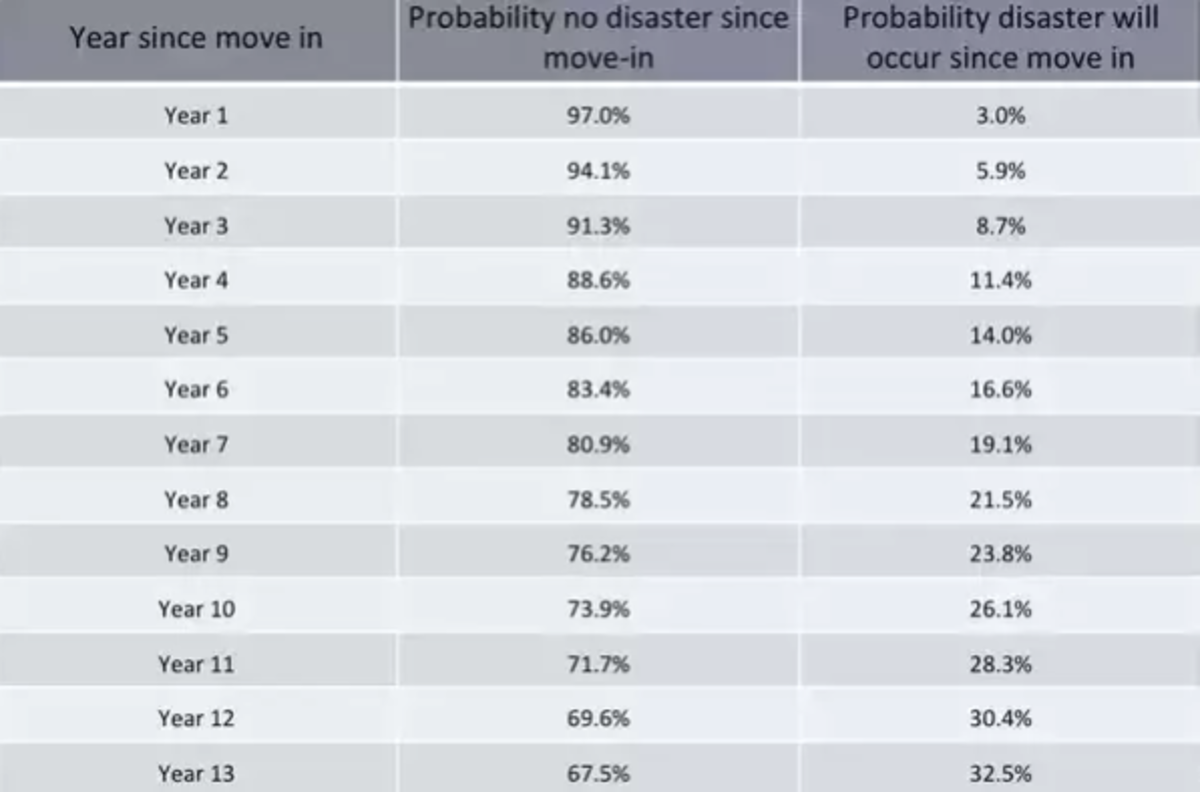

Notice how the probability of the disasters occurring is steadily rising.

Now plotting these values graphically you can find the breakpoint( the point where the probability you’ve been hit with either disaster exceeds the probability you haven't) is at year 23 .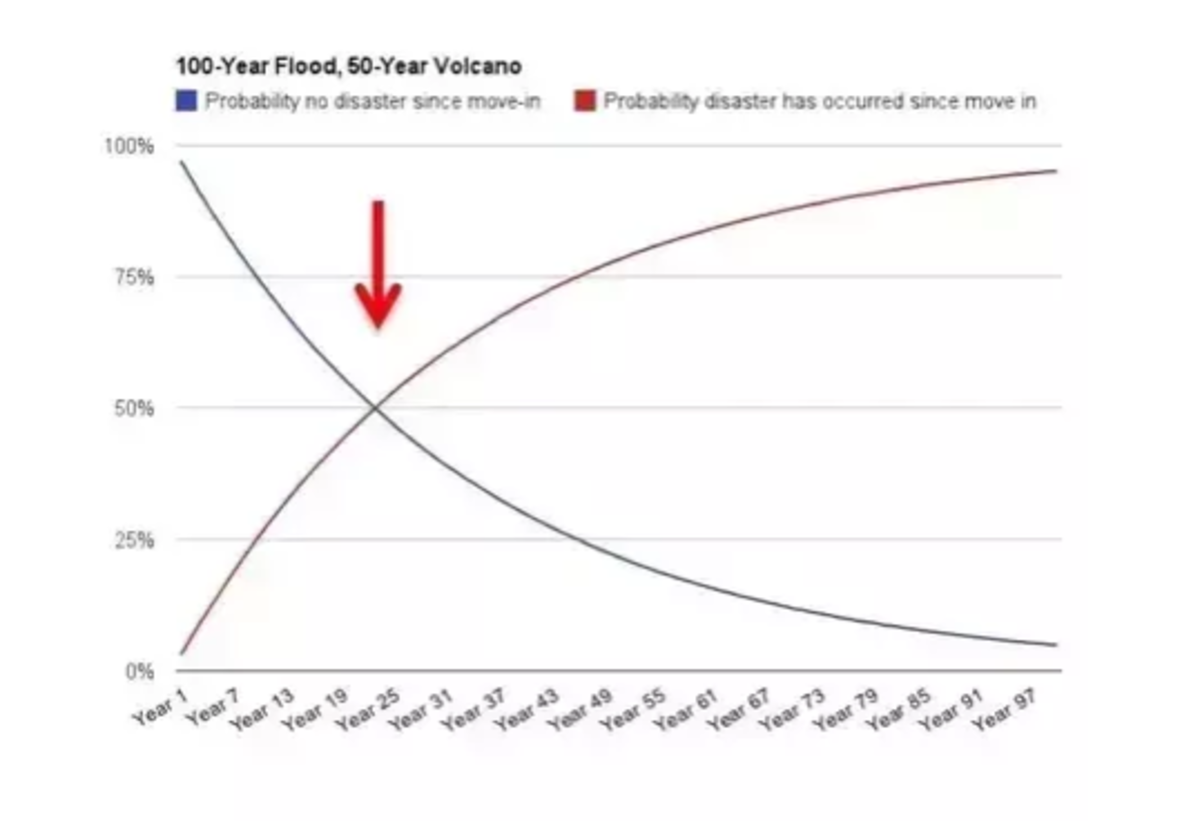

How can you use this idea?

-Well, consider the situation of purchasing flood insurance

-You can calculate your expected payout and compare this expected accumulated costs to figure out whether purchasing the insurance is worth or not else you could just save the money on your own.

-This is a basic example of what actuaries and insurance companies do to calculate your rates.

The probability $P_i ( V \,\cup\, T )$ of experiencing at least one of the events ( events not mutually exclusive) in a year $i$ ( volcanic eruption $V$ , tsunami $T$ ) is given by:

$\quad$

$\displaystyle P_i ( D ) = P_i ( V \,\cup\, T ) = P_i ( V ) + P_i ( T ) - P_i ( V \, \cap\, T )$

$\quad$

$\displaystyle P_i ( D ) = \frac{1}{100} + \frac{1}{50} - \frac{1}{50 \cdot 100 } = \frac{149}{5000}$

$\quad$

Then the probability of NOT experiencing at least one of these two in any given year is given by:

$\quad$

$\displaystyle P_i ( D^c ) = 1 - P_i ( D ) = \frac{4851}{5000}$

$\quad$

The probability of NOT experiencing at least one of the events in a sequence of $n$ years is given by:

$\quad$

$\displaystyle \prod_{i = 1}^{n} P_i(D^c) = ( P (D^c ) )^n$

$\quad$

50% certainty of seeing an event $D$ is that same as 50% certainty of not seeing the event $D$ .

$\quad$

$\displaystyle ( P ( D^c ) )^n = \frac{1}{2}$

$\quad$

$\left( \frac{4851}{5000} \right)^n = \frac{1}{2}$

$\text{ln} \left( \left( \frac{4851}{5000} \right)^n \right) = \text{ln} \left( \frac{1}{2} \right)$

$\quad$

Finally, the number of years before you are 50% sure you will see at least one event ( volcanic eruption or tsunami ) is given by:

$\quad$

$\displaystyle n = \frac{ \text{ln} \left( \frac{1}{2} \right) }{ \text{ln} \left( \frac{4851}{5000} \right) } \approx \text{22.92} \approx \text{23}$