Tucking an ellipse between two rays
You have two rays originating at the origin of the Cartesian plane. These are shown by the green line segments in the figure below. The first makes an angle of with the positive -axis, while the other one makes an angle of with the positive -axis. You also have an ellipse having a semi-major axis length of units and a semi-minor axis length of units. The ellipse major axis makes an angle of with the positive -axis. You want to move this ellipse around while keeping its orientation, such that at the end of your maneuvers, the ellipse becomes tangent to both rays. If the center of the ellipse, once in place, is , and the tangent points with the two rays (the green dots) are and , then enter the value of .
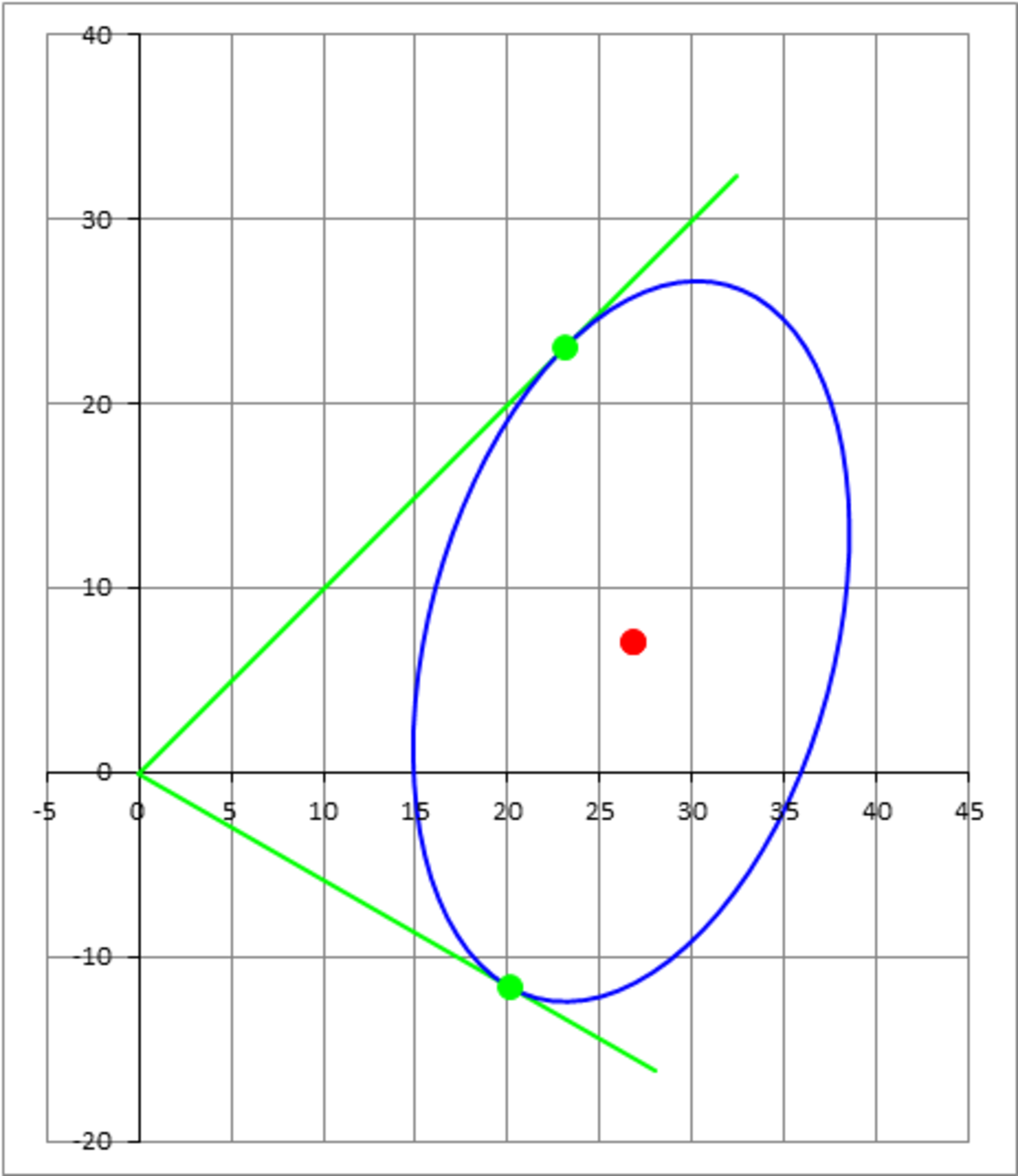
The answer is 88473.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let θ 1 = − 3 0 ∘ = − 6 π and θ 2 = 4 5 ∘ = 4 π . Define the unit vectors along the rays and perpendicular to the rays as
u 1 = [ cos θ 1 sin θ 1 ] , u 2 = [ sin θ 1 − cos θ 1 ] , u 3 = [ cos θ 2 sin θ 2 ] , u 4 = [ − sin θ 2 cos θ 2 ]
Note that the perpendicular vectors u 2 and u 4 are pointing outward from the region that is bounded in between the two rays.
The equation of our ellipse is ( r − C ) T R D R T ( r − C ) = 1 , where the diagonal matrix D = diag { 2 0 2 1 , 1 1 2 1 } , and matrix R is a rotation matrix by an angle of ϕ = 7 5 ∘ = 1 2 5 π and is given by
R = [ cos ϕ sin ϕ − sin ϕ cos ϕ ]
And r is the coordinate vector of a point on the ellipse, while C is the coordinate vector of the center of the ellipse.
The gradient vector which points normal to the ellipse in an outward direction from the ellipse is given by ∇ ( r ) = 2 R D R T ( r − c ) . At the tangent points with the two rays we have
R D R T ( r 1 − C ) = α u 2 and R D R T ( r 2 − C ) = β u 4 , where α > 0 , β > 0 .
Solving for ( r 1 − C ) , we obtain, r 1 − C = α R D − 1 R T u 2 and similarly r 2 − C = β R D − 1 R T u 4
Substituting these into the equation of the ellipse, we deduce that
α = u 2 T R D − 1 R T u 2 1
β = u 4 T R D − 1 R T u 4 1
Now that α and β are known, we can proceed to find the center C and the tangent points r 1 and r 2 .
Here we note that r 1 is along the vector u 1 , therefore, by premultiplying by the perpendicular vector it is eliminated.
u 2 T ( r 1 − C ) = 0 − u 2 T C = α u 2 T R D − 1 R u 2 = u 2 T R D − 1 R T u 2
Where the right hand side of the above equation is known. Similarly, we can write a second linear equation in the unknown vector C , for the the second ray,
u 4 T ( r 2 − C ) = 0 − u 4 T C = β u 4 T R D − 1 R u 4 = u 4 T R D − 1 R T u 4
So that now we have the following linear system
A C = b
where the matrix A is given by
A = [ − u 2 T − u 4 T ]
and the vector b is
b = [ u 2 T R D − 1 R T u 2 u 4 T R D − 1 R T u 4 ]
And this can solved readily for the unknown coordinate vector of the center C .
Having found the center, the tangent points r 1 and r 2 can be found immediately from the expressions above.
Namely,
r 1 = C + α R D − 1 R T u 2
and
r 2 = C + β R D − 1 R T u 4
This concludes our calculations. The required sum comes to 8 8 . 4 7 3 , and this makes the answer 8 8 4 7 3 .
Another solution is possible by considering a reference frame having its origin O ′ at the center of the ellipse and with its x ′ axis along the major axis of the ellipse and its y ′ axis along the minor axis. Since the ellipse is rotated by 7 5 ∘ counterclockwise with respect to the global reference frame, then the two tangent rays are rotated by − 7 5 ∘ with respect to its local reference frame O ′ x ′ y ′ . Therefore, the direction vectors of the normals to these rays pointing outward of the ellipse are simply R T u 2 and R T u 4 , where the matrix R is defined above, and premultiplying by its transpose has the effect of rotating u 2 and u 4 by − 7 5 ∘ ( i.e. 7 5 ∘ clockwise ). Now the equation of the ellipse with respect to its local reference frame is r ′ T D r ′ = 1 , so that its gradient (which is normal to it) is ∇ ( r ′ ) = 2 D r ′ , and this means that at the two tangent points, we have, respectively,
r 1 ′ = α D − 1 R T u 2 and r 2 ′ = β D − 1 R T u 4 , α > 0 , β > 0
So that, upon substituting this into the equation of the ellipse, yields the same expressions for α and β as above. Thus , we now have the tangent point r 1 ′ and r 2 ′ . What is left is to find the intersection point P 0 between the two tangents at r 1 and r 2 . And for that we can write the linear system in the parameters t and s as follows
P 0 = r 1 ′ + t R T u 1 = r 2 ′ + s R T u 3
and this can be solved for t and s , and thus we've obtained P 0 .
At the final step, and since the coordinates required are in the global frame, we have to relate the two frames O ′ x ′ y ′ and the global frame O x y . Note the point P 0 is the origin of the global system, and that the global frame is rotated by R T with respect to the local frame. The relation between the two frames is
r ′ = P 0 + R T r
so that,
r = R ( r ′ − P 0 )
And this concludes the second method.
One can see that the results will be identical, if one considers the solution for P 0 in the second method. We have,
P 0 = r 1 ′ + t R T u 1 = r 2 ′ + s R T u 3
Premultiplying by R through, we obtain,
R P 0 = R r 1 ′ + t u 1 = R r 2 ′ + s u 3
Premultiplying by u 2 T ,
u 2 T R P 0 = u 2 T R r 1 ′ = α u 2 T R D − 1 R T u 2 = u 2 T R D − 1 R T u 2
similarly,
u 4 T R P 0 = u 4 T R D − 1 R T u 4
Writing the above two equations as a linear system, and comparing with the linear system obtained in the first method, one deduces that C = − R P 0 . In addition, R ( r 1 ′ − P 0 ) = R r 1 ′ + C = r 1 and R ( r 2 ′ − P 0 ) = R r 2 ′ + C = r 2 .