Tunnel Snake

Geometry Level 5

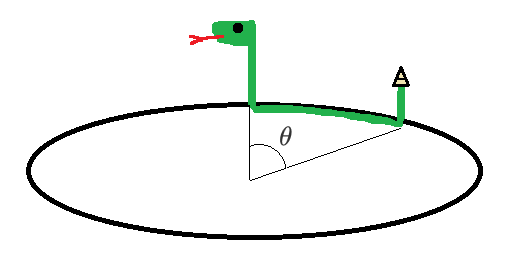
A snake with body length 1 from head to tail has made an underground tunnel in the shape of a unit circle. Starting from inside the tunnel, the snake pokes 1 3 \frac{1}{3} of its length (including its head) straight upwards out of the tunnel at some location. The snake then pokes its tail (and some length of its body) straight upwards out of the tunnel somewhere else. The rest of the snake's body remains within the tunnel.

The two poking locations are separated by an angle of θ . \theta. What value of θ \theta (in degrees) minimizes the straight-line distance from the snake's head to its tail?

Details and Assumptions:

  1. The straight-line head/tail distance depends on three spatial dimensions.
  2. The snake does not coil or contort within the tunnel.
  3. The tunnel is just below the ground surface.
  4. Simply treat the head and tail as the two ends of the snake.


The answer is 9.5715.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Jeremy Galvagni
Jul 26, 2018

I'm not sure this can be done without calculus, so I suggest a category change.

Let's coordinatize: The circle will be centered at the origin in the x-y plane and the z-coordinate will be the height. If we put the snake's head hole on the x-axis, the head has coordinates ( 1 , 0 , 1 3 ) (1,0,\frac{1}{3}) .

Let the portion of the snake's body inside the tunnel be θ \theta and oriented counterclockwise (opposite from the picture) so the tail has coordinates ( cos ⁡ θ , sin ⁡ θ , 2 3 − θ ) (\cos{\theta},\sin{\theta},\frac{2}{3}-\theta)

The distance formula becomes d ( θ ) = ( cos ⁡ θ − 1 ) 2 + ( sin ⁡ θ − 0 ) 2 + ( 2 3 − θ = 1 3 ) 2 = 2 − 2 cos ⁡ θ + ( 1 3 − θ ) 2 d(\theta)=\sqrt{(\cos{\theta}-1)^{2}+(\sin{\theta}-0)^{2}+(\frac{2}{3}-\theta=\frac{1}{3})^{2}}=\sqrt{2-2\cos{\theta}+(\frac{1}{3}-\theta)^{2}}

A quick graph shows this has a minimum at θ ≈ 0.167055 \theta \approx 0.167055 radians or 9.571546 \boxed{9.571546} degrees.

Can we get an exact or 'better' solution?

d ′ ( θ ) = sin ⁡ θ − 1 3 + θ 2 − 2 cos ⁡ θ + ( 1 3 − θ ) 2 d'(\theta)=\frac{\sin{\theta}-\frac{1}{3}+\theta}{\sqrt{2-2\cos{\theta}+(\frac{1}{3}-\theta)^{2}}}

For this to equal zero, the numerator must equal zero so we could try solving sin ⁡ θ = 1 3 − θ \sin{\theta}=\frac{1}{3}-\theta . However, this type of equation doesn't generally have an exact form.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Thanks for the solution. I did it the same way. Maybe this should change categories.

Steven Chase - 2 years, 10 months ago
Nicola Mignoni
Jul 26, 2018

Let's put the system in a x y z xyz -coordinate space. Let the tunnel be described by the equation x 2 + y 2 = 1 x^2+y^2=1 . The snake is 'divided' in three parts:

  • the 'head' h = 1 3 \displaystyle h=\frac{1}{3}
  • the 'tail' t \displaystyle t
  • the 'body' b = 2 3 − t \displaystyle b=\frac{2}{3}-t .

Since the snake has lenght 1 1 , we'll have that h + b + t = 1 h+b+t=1 . Let be the point from which the tail pokes

T = ( 1 , 0 , t ) \displaystyle T=(1,0,t)

and the one from which the head pokes

H = ( cos ⁡ θ , sin ⁡ θ , 1 3 ) \displaystyle H=\bigg(\cos{\theta},\sin{\theta},\frac{1}{3}\bigg) .

The 'body' lies on an arc of the circumference, so b = θ = 2 3 − t \displaystyle b=\theta=\frac{2}{3}-t . Hence

T = ( 1 , 0 , 2 3 − θ ) \displaystyle T=\bigg(1,0,\frac{2}{3}-\theta\bigg)

H = ( cos ⁡ θ , sin ⁡ θ , 1 3 ) \displaystyle H=\bigg(\cos{\theta},\sin{\theta},\frac{1}{3}\bigg) .

The distance to minimize is

H T ‾ = D ( θ ) = ( cos ⁡ θ − 1 ) 2 + sin ⁡ θ 2 + ( θ − 1 3 ) 2 = 19 9 − 2 cos ⁡ θ + θ 2 − 2 3 θ \displaystyle \overline{HT}=D(\theta)=\sqrt{(\cos{\theta}-1)^2+\sin{\theta}^2+\bigg(\theta-\frac{1}{3}\bigg)^2}=\sqrt{\frac{19}{9}-2\cos{\theta}+\theta^2-\frac{2}{3}\theta}

d D d θ = 0 ⟹ 3 θ + 3 sin ⁡ θ − 1 = 0 ⟹ θ ≈ 0.16705 rad . \displaystyle \frac{dD}{d\theta}=0 \hspace{5pt} \Longrightarrow \hspace{5pt} 3\theta+3\sin{\theta}-1=0 \hspace{5pt} \Longrightarrow \hspace{5pt} \theta \approx 0.16705 \hspace{3pt} \text{rad}.

Eventually, in degrees

θ ≈ 9.571 ° \theta \approx \boxed{9.571°}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...