Turning off the light
There is a light in another room that can be in one of three states: blue , red , or off .
In your room, you have two buttons numbered 1 and 2 that control the state of the light. The state of light changes according to the diagram below.
- If you press button 1, then the light changes to the next state clockwise around the diagram.
- If you press button 2 while the light is blue or red , the state of the light will not change.
- If you press button 2 while the light is off , the light will change to blue .
You want to make sure that the light is off , but since the light is in another room, you do not know what state the light is currently in.
What is the shortest sequence of button presses that will guarantee that the light will be off ?
Note : Enter your answer as a sequence of digits in order. For example, if you believe the sequence is {1, 2, 1, 2, 1}, then enter 1 2 1 2 1 .
The answer is 211211.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Moderator note:
Having a clear simple presentation of the problem greatly helps us to solve it. In this case, all that we needed to do was to enumerate the states and possible transitions between them.
This is an absolutely wonderful approach
This is... Brilliant !
Thanks! but can you please explain how each vertex represent the possible states? (The hexagon for example)
Log in to reply
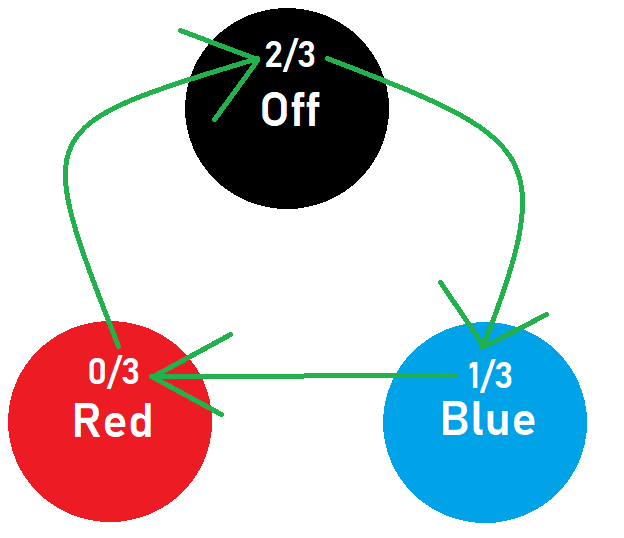
The hexagon means: "At this point RBO, the light might be red, blue, or off."
After pushing button 2, if the light had been off it is now blue. Therefore we know now the light is red or blue. This is represented by the purple triangle BR.
And so on.
To clarify, the elements in my drawing do not represent the states of the light, but the states of our knowledge about the light.
amazing. I admire the simplicity and succinct use of graphics
2 reduces 3 possibilities into 2 - red or blue .
Pressing 1 twice puts these possibles into off and blue locations.
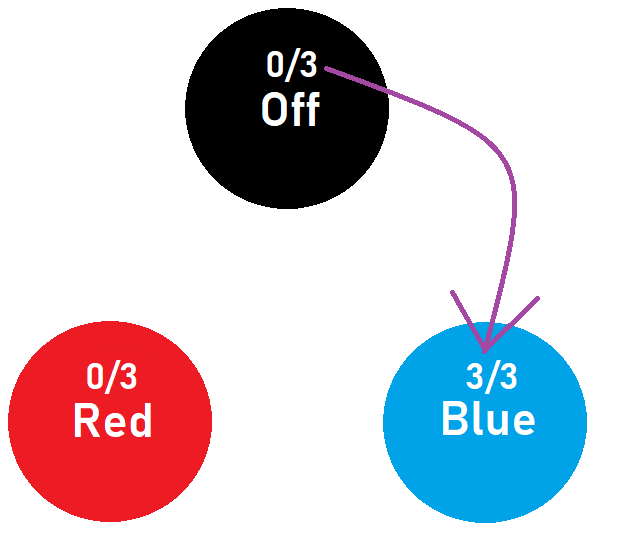
2 reduces the two possibilities to one - blue .
Pressing 1 twice puts this possibility to off .
The problem should state the format in which the answer is to be typed in.
This is how I solved it
how do you prove there is no shorter solution?
Log in to reply
Three possibilities are to be reduced to one. There is only one way to decrease the number of possibilities, using 2 to move "off" to "blue." So 2 has to be used 2 times. 1 has to be used as many times as needed to get the 2 to do its job. This is the lowest number of times it needs to be done.
Neat explanation in words:)
Simplest explanation. Thank you.
^Solution was made before this question got edited, a push is a 1 and a hold is a 2^
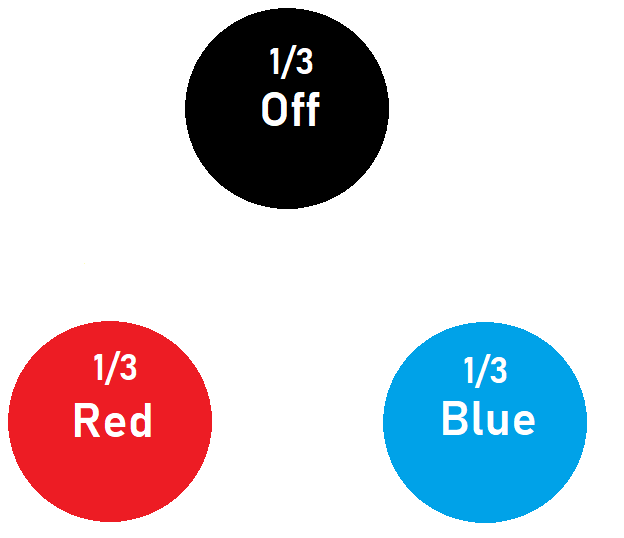
To start off with assume that there is a 3 1 probability of the light being in one of any of the 3 states.
Pushing the button causes all RED lights to become OFF, all OFF lights to become BLUE and all BLUE lights to become RED. This means that the probability of RED will be transferred to OFF, the probability of OFF will be transferred to BLUE and the probability of BLUE will be transferred to RED, which means that pushing the button essentially takes the probability of each state and passes it on to the next state. For this reason starting by pushing the button doesn't help you at all as the 3 1 probability is just being 'passed around the states'.
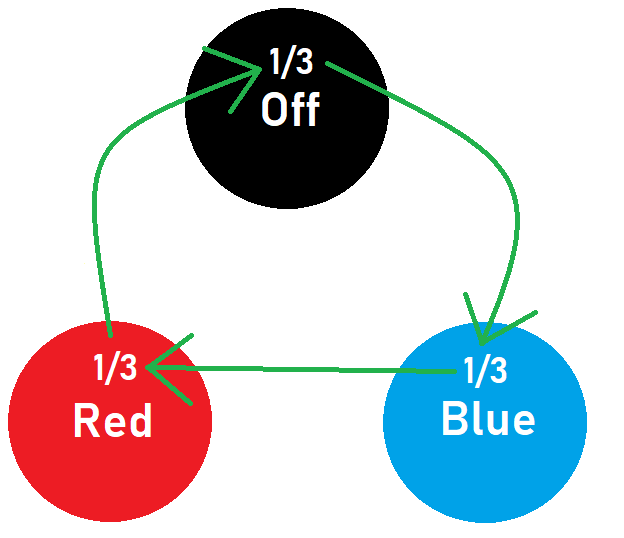
Similar to the way that leading zeros do not affect the value of an integer (i.e. 000563 = 563) starting by pressing the button any number of times will not affect the outcome. For this reason the only way to change the outcome from a 3 1 probability of the light being in any one of the 3 states the first action must be to hold the button.
Holding the button doesn't affect the probability of the light being RED as all lights that are RED will stay RED when you hold the button and no lights will turn from BLUE to RED when you hold the button. The probability of the light being BLUE or OFF, however do change. The probability of the light being OFF is now 3 0 (or just 0%) as all lights in the OFF state will turn to BLUE when you hold the button and no RED lights will change to the OFF state when you hold the button. Because the probability of lights being in the OFF state changes and the probability of lights being in the RED state doesn't change the probability of lights being in the BLUE state must change. When you hold the button all BLUE lights will stay BLUE, however all OFF lights will turn to BLUE so the 3 1 probability of lights being in the OFF state is transferred to the BLUE state, causing the BLUE state's probability to become 3 2 .
All of this can be boiled down to saying that holding the button takes the probability of the OFF state and adds it to the probability of the BLUE state.
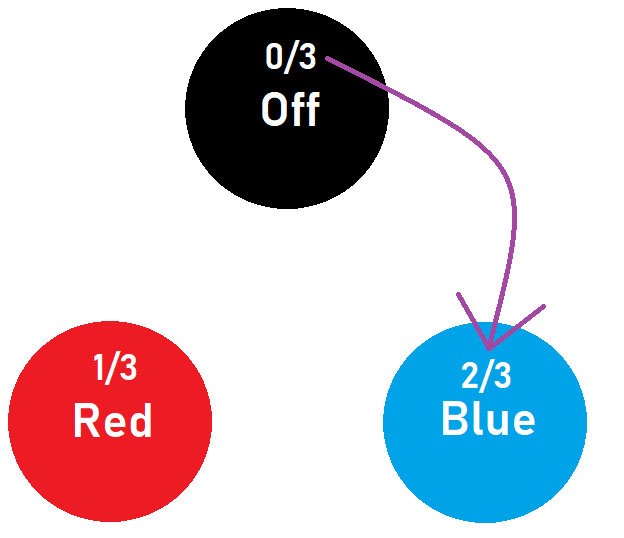
Now we know that all lights must be either BLUE or RED. We also know that all we can do with the probabilities is pass them from each state to the next (by pushing the button) or take the probabilities from the OFF state and add them to the BLUE state (by holding the button). To be able to know what the final state of the light will be we will have to group all of the probabilities together so that one state has a 3 3 (or just 100%) probability. The only way we can group probabilities together is by taking the OFF probability and adding it to the BLUE probability so we want to get the 2 current non-zero probabilities (RED and BLUE) and pass them onto the OFF and BLUE states (allowing us to have a 3 1 probability of the light being in the BLUE state).
To pass these probabilities to the correct states we must push the button 2 times.
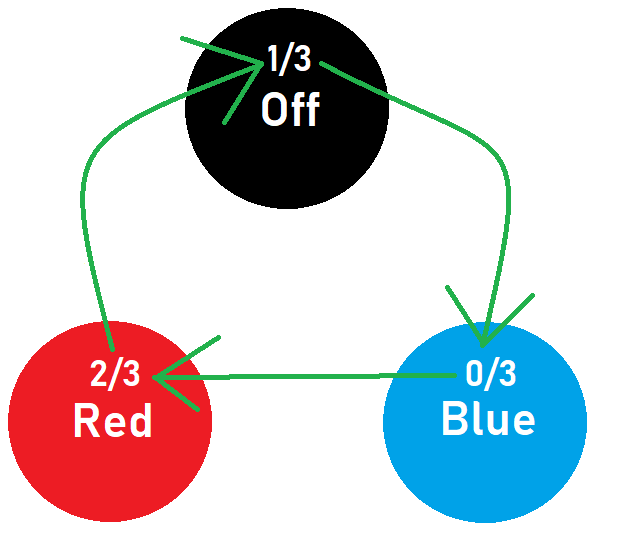
Now that we have the 2 remaining non-zero probabilities at the OFF and BLUE states we can combine them into a 3 3 probability at the BLUE state by holding the button.
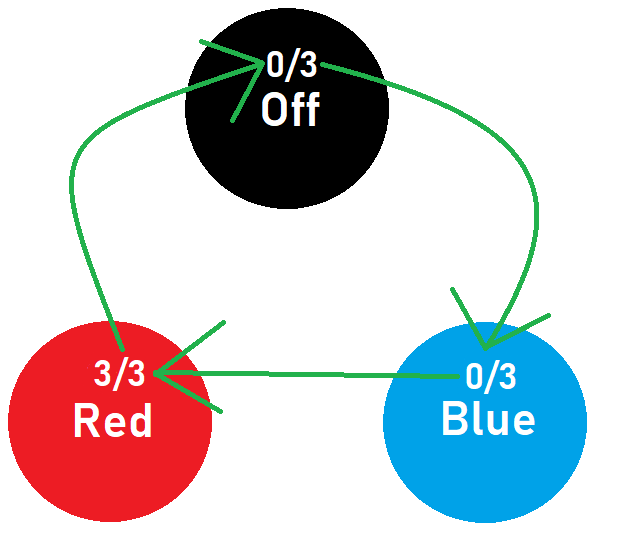
We now know that no matter what the starting state of the light is, if we follow the steps we just went through the state of the light will always be BLUE. To finish off the puzzle we have to ensure that the state of the LIGHT will always be OFF, to do this we simply have to push the button 2 times.
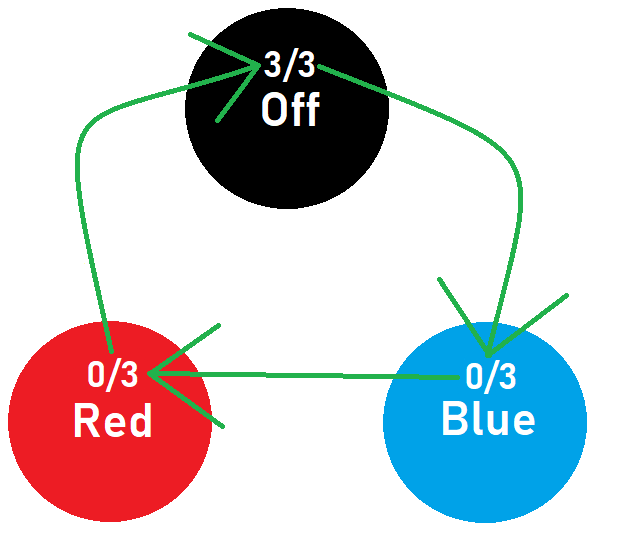
So by following the pattern 'Hold, Push, Push, Hold, Push, Push', we can ensure that the final state of the light will be OFF. This answer also works when the probabilities of each state are different as the probabilities are all eventually added together to a total of 1 regardless of individual probabilities and 'passed' to the OFF state (which means that you can assume any values for the probabilities of each state when starting to solve this problem as long as they all add up to 1).
Converting the above pattern into 0 for a push and 1 for a hold, the pattern would look like 100100.
WHat a long solution! I appreciate the input, but don't get the whole probability part. It's all about counting and getting patterns 'in sync',
Nothing is said about probabilities.... only possibilities.
If you're looking for a quick, simple answer, check Arjen's. This is just the way that allowed me to get to the right answer, however i get that talking about possibilities instead of assigning probabilies to the states may make more sense.
Can you make '6' an acceptable answer next time? I got it first time but spent ages trying to figure out why my answer wasn't being accepted... great puzzle though.
Log in to reply
I made the same mistake, putting 6 in and not the1 or 2 sequence of the buttons.
I actually really like this solution
Step 1. Transform unknown state to a known state with two bulbs.
Step 2. Transform two bulb state to a two bulb state that can become a known single bulb with a single button.
Step 3. Obtain the known single bulb.
Step 4. Cycle the single bulb to off.

There are two possibilities for each step. Let's look at it step by step, assuming that there is indeed an actual optimal solution. Notice our priorities: we want to make actual progress by decreasing the possibilities of the state of the light to 1 and not reverting or staying in the same situation.
At the first step, the light can be either red, blue, or off. If we press button 1, then the light can still be either red, blue, or off. This doesn't help a bit. So, we have to press button 2, decreasing the possibilities of the state to either red or blue.
At the second step, if we press button 2, nothing will change. Again, this doesn't help us, and we will have to press button 1. This means that the light can now be either red or off.
At the third step, if we press button 2, the light will be either red or blue. This reverts us back to the state after the first step, indicating that this route is useless. Thus, we have to press button 1 in order to make any progress. The light is now either off or blue.
At the fourth step, notice if we press button 2, the light will have to be blue. Voila! We found it. Just to be sure, see what happens when we press button 1: the light becomes either red or blue, which reverts us to the case after step one.
Now, the shortest route from a blue light to an off light is to press button 1 twice. Therefore, our steps are 211211.
That was the reasoning I used as well.
The following Python program uses a nice recursive function called
cycle
, which accepts an integer with the digits
1
or
2
and a state, either
"Off"
,
"Red"
or
"Blue"
. It then initialises a variable
integer
, which is incremented during each iteration of an infinite
while
-loop, which breaks when our conditions are met. To check if the integer only contains non-null ternary digits, we check if the set difference of its string representation with the set
{"1", "2"}
is empty.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
|
The result is therefore 211211 .
I find it clearer to use a matrix to indicate the process.
Let ∣ i ⟩ = ⎩ ⎨ ⎧ ∣ 0 ⟩ ∣ 1 ⟩ ∣ 2 ⟩ o f f b l u e r e d
A indicates press botton 1 ; B indicates press botton 2.
We need to find an operation sequence F ( A , B ) so that F ( A , B ) ∣ ψ ⟩ = ∣ 0 ⟩ , ∣ ψ ⟩ indicates an arbitary state.
The matrix representation of F ( A , B ) under the basis { ∣ i ⟩ , i = 0 , 1 , 2 } is F i j = ⟨ i ∣ F ∣ j ⟩ = ⟨ i ∣ ∣ 0 ⟩ = δ i 0
F = ⎝ ⎛ 1 1 1 0 0 0 0 0 0 ⎠ ⎞
Similarly, A,B can be represents as matrices:
A = ⎝ ⎛ 0 0 1 1 0 0 0 1 0 ⎠ ⎞ B = ⎝ ⎛ 0 0 0 1 1 0 0 0 1 ⎠ ⎞
There're some rules which make things easier:
A 3 = A B 2 = B
( a b c ) ⋅ A = ( c a b )
( a b c ) ⋅ B = ( 0 a + b c )
a , b , c are 3 × 1 matrices
In the next table,all possible F(A,B) are shown in order of length:
| Length of F(A,B) | expression of F(A,B) |
| 1 | A and B |
| 2 | AB and BA |
| 3 | AAB,ABA,BAA,BAB |
| 4 | BAAB,AABA,BABA,ABAA,ABAB |
After calculation, B A A B = ( 0 1 0 )
So the shortest operation sequence is BAABAA
Think of it as function composition.
These operations can be considered as two functions. Let's use three numbers as states of the light,1->off,2->red,3->blue,
Thus the button 1 is a function f where:
| x | f(x) |
| 1 | 2 |
| 2 | 3 |
| 3 | 1 |
the button 2 is a function g where:
| x | g(x) |
| 1 | 2 |
| 2 | 2 |
| 3 | 3 |
Now the problem is translated into mathematical language:
Given the function f and g,find the shortest composition of function f and g called h,such that ∀x∈{1,2,3},h(x)=1;
By using inverse functions,it's easy to find out the shortest composition of f ang g:
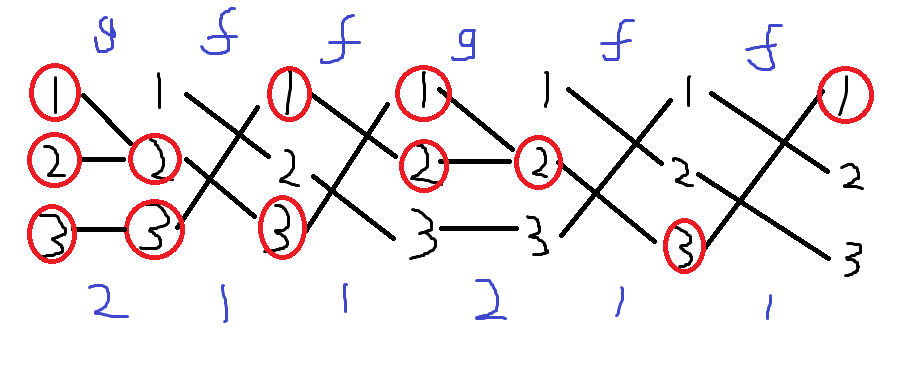
So the answer is 211211.
How about think in an reverse way. We start at an position "off". Every switch do the thing reverse. The puzzle is then to make the state totally "unknown"(3 possible state, Blue , Red, Off).
Now we start at position "off": it must be switched from Red. so the last button pressed is "1".
The same as "off" Red: it must be switched from Blue, or we'll do nothing. So the second last button pressed is "1".
From blue, button 2 can help us create 2 possible state: (off and Blue), while button 1 can't do anything. so it has to be "2".
Now we need another possible state Red. so this time it can't be button "2" because it won't create a possibly state Red. So it should only be "1".
Now the possible state is (Red or Off). we need a "blue". We had no choice but use again button "1".
Now the possible state is (Red or Blue). By button "2", we can create all the three possibility. So we can finish the new puzzle by pressing "2".
Now watch the last line. put it in an reversed way. It is the anwser to the original puzzle: 211211. And definitely the shortest solution.
We have three possible initial states, blue, red, or off. The goal is to turn them off. Notice that the only way to cause a difference is going from [Off] to [Blue] by pressing #2. It will allow [Off] to advance while pausing red and blue.
| Initial State | Blue | Red | Off |
| Button# | SC1 | SC2 | SC3 |
| 2 | Blue | Red | Blue |
| 1 | Red | Off | Red |
| 1 | Off | Blue | Off |
| 2 | Blue | Blue | Blue |
| 1 | Red | Red | Red |
| 1 | Off | Off | Off |
Steps:-
1) [#2] : since pressing #1 will advance each state to the next state (rotation).
2) [#1] : since pressing #2 will not change the current states (pause).
3) [#1] : to move all states to either [Off] or [Blue].
4) [#2] : to change all states to blue.
5) Press [#1] twice to turn them off.
Starting may be any of O, R, B.
We are aiming for B, B, B as then 1,1 must give O.
If we can get to no R, then B, B, B will be achieved with a 2.
There is no point starting with 1 > B, R, O no progress.
So must start 2 to give options now as > B, R, B.
No point in another 2 as nothing will change.
So must be 1 > R, O, R.
To remove all R, must be 1 again > O, B, O.
Now 2 > B, B, B.
and 1 > R, R, R.
and 1 > O, O, O so light must be off.
So solution is 211211
Answer = 211211
Initial possible state(s) = 3 (reduce it to 1)
If possible state = 1 = achieved, AND
If that state is not = off, then change it to off.
Now, pressing:
1 = Possible states still = 3 = Error
2 = Reduces us to either red (R) and blue (B).
2 = No difference = Error
1 = Blue changes to red and red changes to off.
2 = Red remains red and off changes to blue which takes us back to where we started = Error
1 = Red changes to off and off changes to blue.
2 = Off changes to blue and blue remains blue possible state = 1 = achieved
Now, just change blue to off i.e. 11.
If we can be sure that the light is in either blue or off state; then by pressing switch 2 we can make sure the right is in blue state....Then pressing switch 1 two times we can make sure the light is off....Now how we make sure the light is either blue or off state??!!!...Notice in 1st step if we press switch 2 then we can make sure that the is on..i.e it is either in red or blue state...Now by pressing 1 two times we can make sure the light is in blue or off state (if the light was red then it will be blue.If the light was blue then it will be in off state)....So now we sure that the light is either blue or off state...Now by proceeding as mentioned above we can make sure the light is turned off...so the sequence is 211211..
In the following graph, each vertex represents the possible states of the light. We wish to find the shortest path from RBO to O. The route is obvious once all transitions have been drawn (black = 1, green = 2).