Tweaking P and Q

Electricity and Magnetism Level 3

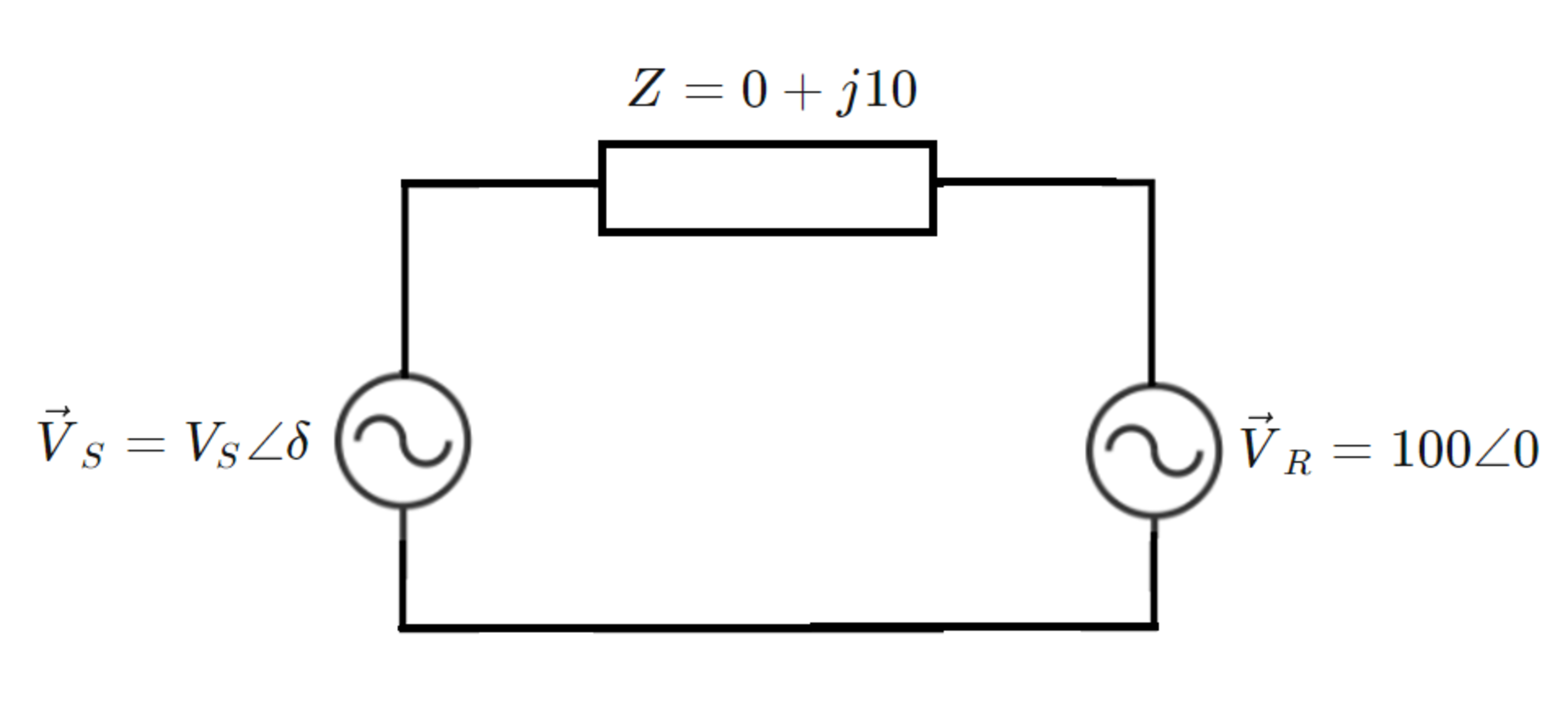
Two ideal AC voltage sources are connected to the ends of a transmission line segment. $V_S$ is the magnitude of the Source $S$ voltage, and $\delta$ is its phase angle in radians.

If $P_R$ is the active power consumed by Source $R$ , and $Q_R$ is the reactive power consumed by Source $R$ , calculate the following sum of partial derivative ratios, with $\delta = \frac{\pi}{9}$ and $V_S = 100$ as baseline numbers.

$\frac{| \partial P_R / \partial \delta | }{ | \partial Q_R / \partial \delta |} + \frac{ | \partial P_R / \partial V_S | }{ | \partial Q_R / \partial V_S | }$

Bonus: What is the significance of each ratio?

The answer is 3.111.

1 solution

Karan Chatrath
Sep 6, 2019

General outline of the solution

The current through the load is:

$I = \frac{\vec{V}_S -\vec{V}_R}{Z}$

The resultant power (consumed by the source R) is the complex number:

$S = \vec{V}_RI = P_R + jQ_R$

Here, $P_R$ and $Q_R$ are functions of $\delta$ and $V_S$ .

The real part of $S$ is the active power while the imaginary part is the reactive power. From here, the required ratio is computed. Each ratio highlights how sensitive the active power component is (relative to the reactive power component) to the given parameters $V_S$ and $\delta$ . A higher ratio (magnitude) means that for a small change in a parameter, the active power changes more relative to the reactive power. I think there might be a better way of interpreting this.

Yeah, that's basically it. The conclusion is that the active power is controlled largely by the voltage angle, and the reactive power is controlled largely by the voltage magnitude. Also, in your expression for $S$ , we need the complex conjugate of the current.

Steven Chase - 1 year, 9 months ago

Tweaking P and Q

The answer is 3.111.

1 solution

0 pending reports