Twin Incircles

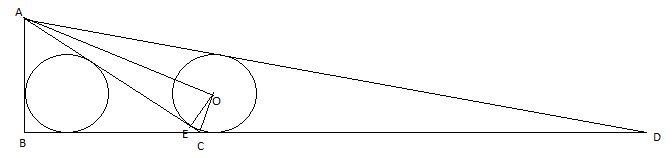
First of all, let's find the measure of the radius of the triangle $\triangle ABC$ .

The easiest way to do so, I believe, is by finding the area of the triangle. Since it's a $(3, 4, 5)$ triangle, we know it's a right triangle and thus its area equals $\frac{3*4}{2} = 6$ . This area can also be calculated by finding the semiperimeter of the triangle, and multiplying it by the radius of the incircle. Let's call this radius r; the semiperimeter of the triangle equals $\frac{3 + 4 + 5}{2} = 6$ . Thus, $6*r = 6$ , and so $r = 1$ .

Now we will adopt a similar procedure with triangle $\triangle ACD$ . I will call $\overline{CD} = a$ and $\overline{AD} = b$ . The area of this triangle equals $\frac{3a}{2}$ ; the reason why is because the segment $\overline{BD}$ is perpendicular to the segment $\overline{AB}$ , the latter of which measures $3$ and is also a height of the triangle $\triangle ACD$ . Also, the semiperimeter of this triangle equals $\frac{a + b + 5}{2}$ , thus $\frac{r*(a + b + 5)}{2} = \frac{3a}{2}$ ; since we know r = 1, we can write the equation as $b = 2a - 5$ .

Now, to find the values of $a$ and $b$ , we can apply Pythagoras' Theorem on the triangle $\triangle ABD$ to yield the following:

$3^{2} + (4 + a)^{2} = b^{2}$

$3^{2} + (4 + a)^{2} = (2a - 5)^{2}$

$9 + (16 + 8a + a^{2}) = (4a^{2} - 20a + 25)$

$3a^{2} - 28a = 0$

$a = 0$ or $a = \frac{28}{3}$

$a$ cannot have a value of zero because it would make $b = -5$ and we'd have a negative length, which is absurd; thus, we find that $a = \frac{28}{3}$ , and then $b = 2*\frac{28}{3} - 5 = \frac{56-15}{3} = \frac{41}{3}$ .

Thus, the ratio $\frac{\overline{AD}}{\overline{CD}} = \frac{41}{28}$ , and therefore the difference sought is $41 - 28 = 13$

Solution provided by Alexandre Miquilino is far more elegant than what follows. I am including this solution to show that when it comes to triangles, plodding tends to get you there even if you don't know some tricks, such as the connection between area of a triangle, its perimeter, and the radius of its incircle.

You can get angle BCA from dimensions of that triangle. This will determine angle ACD and therefore its half sized angle ACO. From this and the distance EO being 1 the distance EC can be calculated. Distance AE will be what's left of 5 after subtracting EC, and together with EO being 1 it will give us the angle EAO. Angle BAD will then be the size of angle BAC (from triangle BAC) plus twice the size of angle EAO. Triangle ABD will then give us the sides AD and BD, from which the rest follows easily.