Twinkle Twinkle Little Star

What is the value of a + b + c + d + e in degrees?
The answer is 180.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
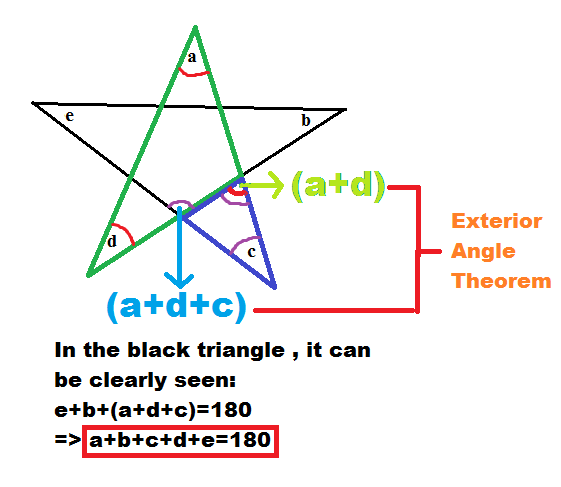
Great solution!
There's another interesting approach if we assume that the 5 points of the star lie on a circle. Anyone want to discuss this one?
Log in to reply
5 inscribed angles. 1/2 the measure of their respective arcs.
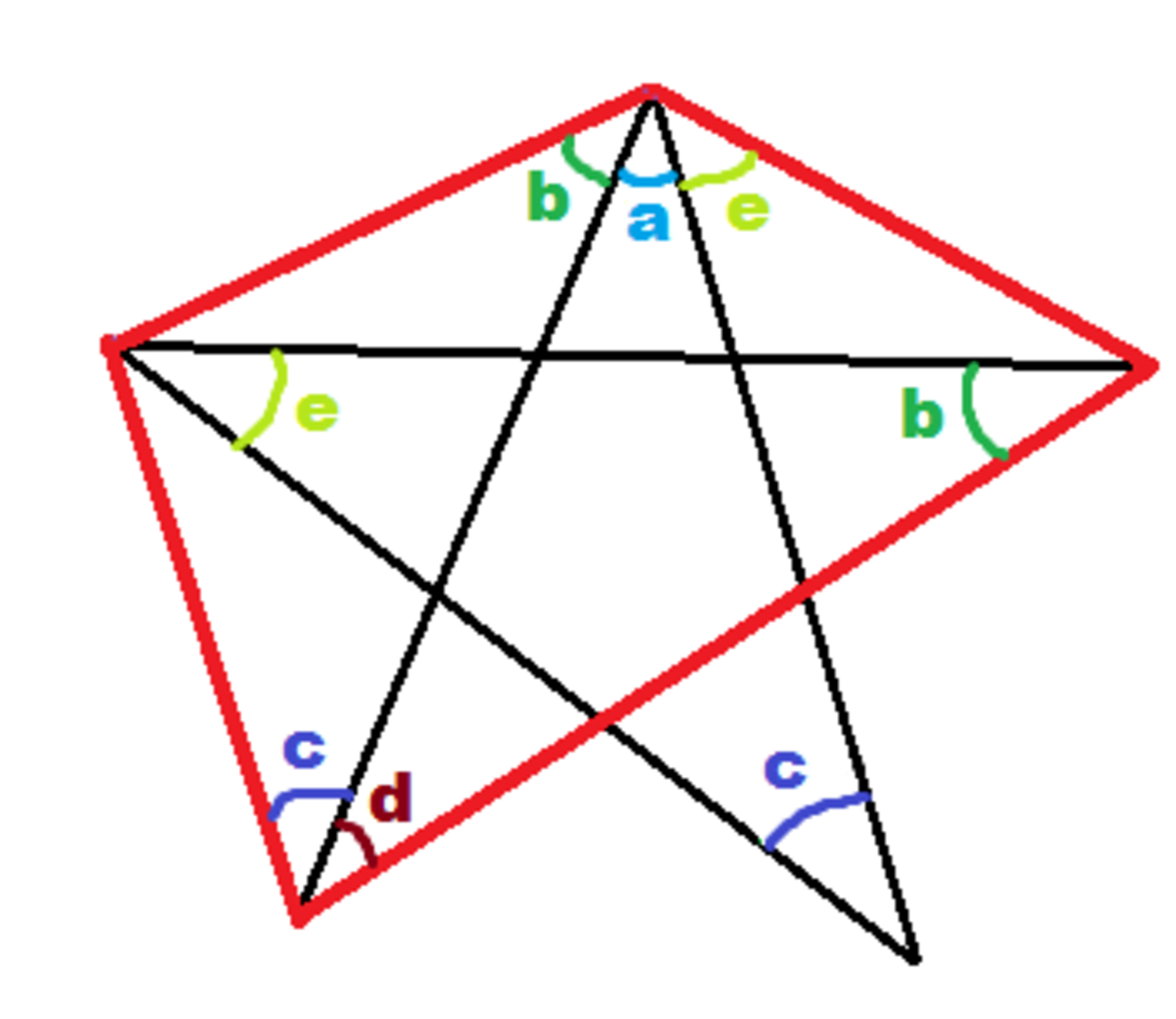
Use the property of angles subtended by same arc and focus on the red quadrilateral. The opposite angles of a cyclic quadrilateral are supplementary , giving us what we require :)
Yeaah i would like to
Check my solution
Great solution nice, simple and clear
SIMPLE UNREADABLE SOLUTION
Create a point in the middle of the pentagon. Then create 5 identical triangles from this point where the 2 points of the pentagon are their base angles.
360 / 5 = 72 (the angle of the middle point of your triangle).
(180 - 72) : 2 = 54 (the base angle of the triangle: half of the inside angle of the pentagon)
360 - 54 × 4 = 144 (the 2 angles of the star's triangle. Why 4? See previous step.)
And finaly
180 - 144 = 36 (the angle of one of the triangles points, in this case of a, b, c, d, e)
5 × 36 = 180
P.S.
Don't judge me for the unreadability of this solution. It's the first time I write a one. Thank you for reading!
congratulations, not seen that it is first time. very simple easy way to explain. every body can understand easily..........regards
The interior angle formula of the a regular polygon is ( n − 2 ) ∗ 1 8 0 ∘ where n is the number of sides, so the sum of the interior angles of the pentagon in the center is ( 5 − 2 ) ∗ 1 8 0 ∘ = 5 4 0 ∘ . It is regular such that the angles are equal so that each interior angle equals 5 5 4 0 ∘ = 1 0 8 ∘ . This lets us find the other two angles of the triangles a, b, c, d, and e since the interior angles of the pentagon and the other angles of the triangles a, b, c, d, and e form straight lines (180 ∘ ) such that the other angles of the triangles a, b, c, d, and e are equal to 1 8 0 ∘ − 1 0 8 ∘ = 7 2 ∘ .
Triangles also have 180 degrees from interior angle formula, which determines that the angles a, b, c, d, and e are equal to 1 8 0 ∘ − 2 ∗ 7 2 ∘ = 3 6 ∘ . Thus the sum of angles a, b, c, d, and e=(5*36^\circ=180^\circ.
I KNEW IT! Reading Chinese Comics will get me somewhere

Omg lol xD
Wow lol, if there is an oscar of best comment ull probably laugh when they'll tell u u got it
Draw a circle that touches the 5 heads of the star A,B,C,D,E
Now every single one of them forms an Inscribed angle
I n s c r i b e d a n g l e = 2 1 i t ′ s c o r r e s p o n d i n g A r c
Thus
∠ A = 2 1 C D
∠ B = 2 1 D E
∠ C = 2 1 E A
∠ D = 2 1 A B
∠ E = 2 1 B C
And since this is a homogenous star (Assumed just to make it easier to solve quickly)
(hint: contains an Regular pentagon in it's core)
Then
∠ A = ∠ B = ∠ C = ∠ D = ∠ E
C D = D E = E A = A B = B C = 5 3 6 0 = 7 2
∠ B = ∠ C = ∠ D = ∠ E = ∠ A = 2 1 × 7 2 = 3 6
So;
∠ A + ∠ B + ∠ C + ∠ D + ∠ E = 5 × ∠ A = 5 × 3 6 = 1 8 0
It'll always be the same answer
In case if it's not a Regular shaped star
Substitute in the below equation by the first 5 equations
C D + D E + E A + A B + B C = 3 6 0
You will get
2 ∠ A + 2 ∠ B + 2 ∠ C + 2 ∠ D + 2 ∠ E = 3 6 0
2 ( ∠ A + ∠ B + ∠ C + ∠ D + ∠ E ) = 3 6 0
∠ A + ∠ B + ∠ C + ∠ D + ∠ E = 2 3 6 0 = 1 8 0
Is that what you meant? Eli Ross
That was my answer to the same problem
Yeah, that's what I was getting at. Nice solution!
Log in to reply
Thank you!,
Now you have awakened a dormant question I had back then ,which is
can we solve it with circle even if non of the points fall in the same circle?, I mean if we draw 5 concentric circles is it possible to find a relationship between the points then?
Just for fun, an alternative solution:
Imagine you start at point a and walk along the figure, passing points c , e , b , d , and back to a .
At each point you turn over an angle of 1 8 0 ∘ − x , where x = a = ⋯ = e . The total angle through which you turn is 5 ( 1 8 0 ∘ − x ) = 9 0 0 ∘ − 5 x .
As you do all this, you turn through two four revolutions: a total of 2 ⋅ 3 6 0 = 7 2 0 ∘ . Thus we may write 9 0 0 ∘ − 5 x = 7 2 0 ∘ . It follows immediately that 5 x = 9 0 0 − 7 2 0 = 1 8 0 ∘ , and that is the answer we are looking for. (And, of course, x = 3 6 ∘ .)
Note: If we had walked the pentagon instead of the star, we would only turn through one revolution. The equation would then be 9 0 0 ∘ − 5 x = 3 6 0 ∘ , from which x = ( 9 0 0 − 3 6 0 ) / 5 = 1 0 8 ∘ . This is the angle between sides of the pentagon.
Since the figure does not have to be regular in any way, you can modify it for convenience. Bring angles e and b up toward angle a. As you do so, the measures of angles e and b approach zero, and you are left with △ ABC with angles adding to 180 degrees.
5 triangles can be made using 2 points of the star and one point of the pentagon. Each point of the pentagon therefore has an angle of 180 - (2 of a/b/c/d/e) degrees. The interior angles of a pentagon add up to 540 degrees, and the 5 points add up to 900 - 2a - 2b - 2c - 2d - 2e.
So 900 - 2(a + b + c + d + e) = 540, so a + b + c + d + e = 180
Th simplest solution is noticing that four sides of the pentagon combined with an arm of the star forms a quadrilateral. Assuming the pentagon is a regular pentagon where each angle is 108 degrees, you can solve for the angle in the arm of the star, denoted as theta.
theta = 360 - 3(108) theta = 36
Multiply theta by 5, and you will get 180.
We know that sum of all exterior angles of the pentagon is 360 and there are 5 triangles on the sides of pentagon. If we think that the base of the triangles are sides of the pentagon ,sum of those all base angles will be [2 sum of exterior angles] which is equal to 360 2 = 720 . Then sum if angles in all 5 triangles is 180*5 = 900 . Then a+b+c+d+e = 900 -720 = 180.
Creat a pentagon by joining the vertices by line segment, divide each vertex angle as 4 equal angles, 1/4 x (540/5) so each is 18, then a=2x18 = 36, b=36, c=36, d==36 & e=36, Then a+b+c+d+e =36 x 5 = 180
Good solution