Twins in the Trigon
The figure above shows two equal circles of radius r that are inscribed inside a triangle with side lengths 3, 4, 5.
The two circles share 1 tangent point.
If r can be expressed as B A , where A and B are coprime positive integers, find A + B .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
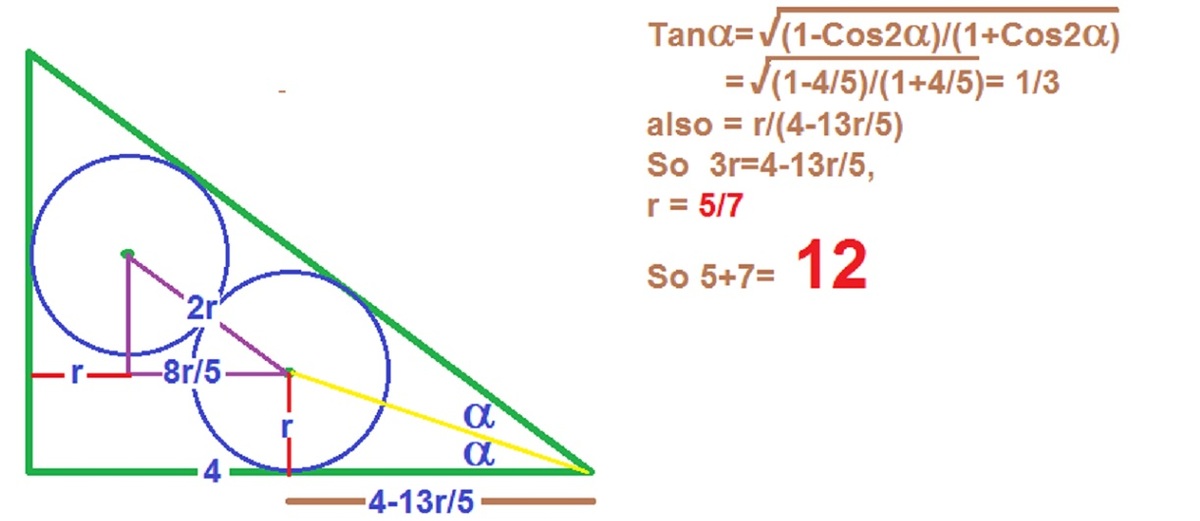
I missed it, since I pressed the "Discuss Solution " by mistake.
Log in to reply
It even happened to me. That's a disgusting feeling.
I think tan(theta) should be y/x, not x/y (though the two end up being interchangeable so it doesn't affect the answer).
How do we know that the top (3-y-r) segments are equal?
Log in to reply
The tangent segments to a circle from an external point are equal.
Tan(theta) should be y/x , they are not interchangeable thanks for pointing out the mistake .
Really, You inspire me to keep my solution pure and geometric and I to my friend. Nice solution +1111. Can I know your profession?
Log in to reply
I'm a Mechanical Engineer.
Log in to reply
Nice And a geometry fan too. Me too but not upto that.
Nyc One! cheers! imitates my approach though ;)
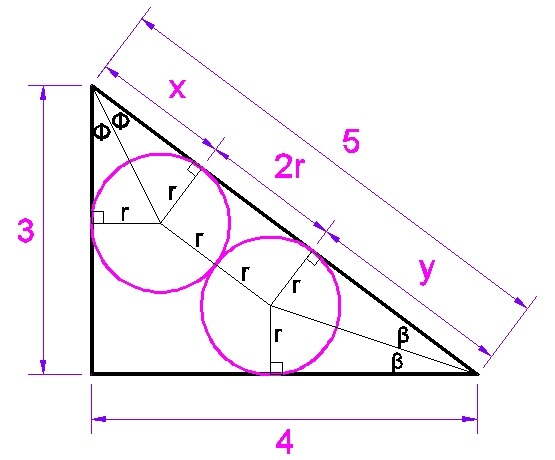 From the figure above,
From the figure above,
t a n 2 Ф = 3 4
Ф = 2 6 . 5 6 5 0 5 1 1 8
x = t a n 2 6 . 5 6 5 0 5 1 1 8 r
t a n 2 β = 4 3
β = 1 8 . 4 3 4 9 4 8 8 2
y = t a n 1 8 . 4 3 4 9 4 8 8 2 r
x + y + 2 r = 5
t a n 2 6 . 5 6 5 0 5 1 1 8 r + t a n 1 8 . 4 3 4 9 4 8 8 2 r + 2 r = 5
7 r = 5
r = 7 5
A + B = 5 + 7 = 1 2
Let's consider the circle tangent to the x -axis. Its center C 1 = ( x , r ) , where r is the radius and x an unknown coordinate. The circle is also tangent to the hypotenuse, which equation is y = − 4 3 x + 3 . Hence, we have
1 6 9 + 1 ∣ 4 3 x + r − 3 ∣ = r ⟹ x = 4 − 3 r
Considering ∣ 4 3 x + r − 3 ∣ = − 4 3 x − r + 3 .
So, C 1 = ( 4 − 3 r , r ) . The same applies for the other center, which coordinates are C 2 = ( r , y ) . Hence
1 6 9 + 1 ∣ 4 3 r + y − 3 ∣ = r ⟹ y = 3 − 2 r
Considering ∣ 4 3 r + y − 3 ∣ = − 4 3 r − y + 3 .
So, C 2 = ( r , 3 − 2 r ) . The tangent circles have the same radius, so the distance between C 1 and C 2 is exactly
( 4 − 3 r − r ) 2 + ( r − 3 + 2 r ) 2 = 2 r ⟹ r = 7 5
considering the smallest of the two possible solutions. Eventually
r = B A = 7 5 ⟹ A + B = 1 2
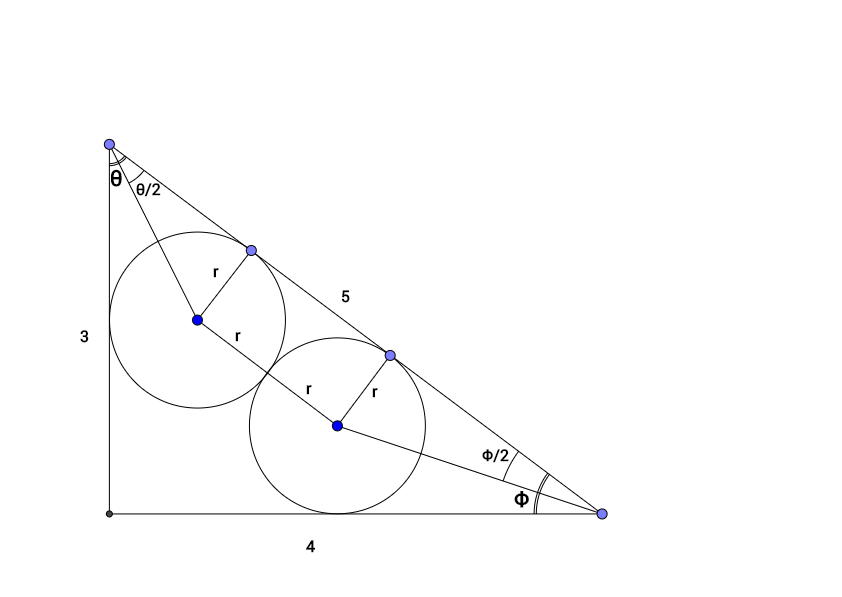
From the figure equating the length of the hypotenuse we get,
2 r + tan 2 θ r + tan 2 ϕ r = 5 → ( 1 )
also we have tan 2 x = sin x 1 − cos x
here sin θ = 5 4 , cos θ = 5 3 , sin ϕ = 5 3 , cos ϕ = 5 4
thus we get, tan 2 θ = 5 4 1 − 5 3 = 2 1
and tan 2 ϕ = 5 3 1 − 5 4 = 3 1
Substituting in ( 1 ) we get,
2 r + 2 r + 3 r = 5 or r = 7 5
thus the required answer is 5 + 7 = 1 2
Very elegant solution to this problem.
3-4-5 Triangles Rule!. Thanks for this simply sophisticated solution...
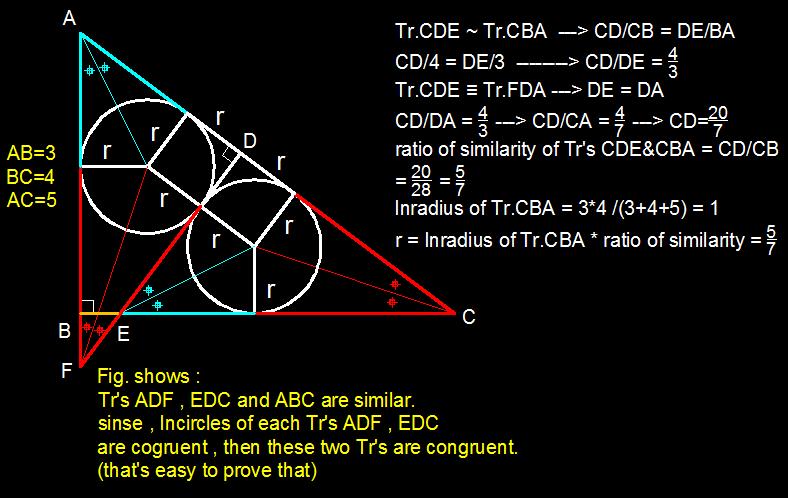
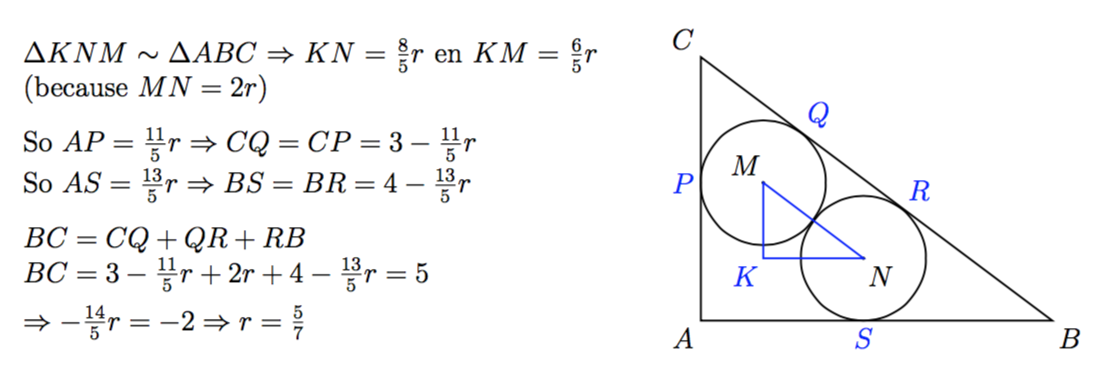
From the figure :
tan θ = 4 3 = x y ( 3 − y − r ) + 2 r + ( 4 − x − r ) = 5 4 y − 3 x = 0 x + y = 2
y = 7 6 , x = 7 8
x 2 + y 2 = 4 r 2 r = 7 5