Equal Areas In Equal Time
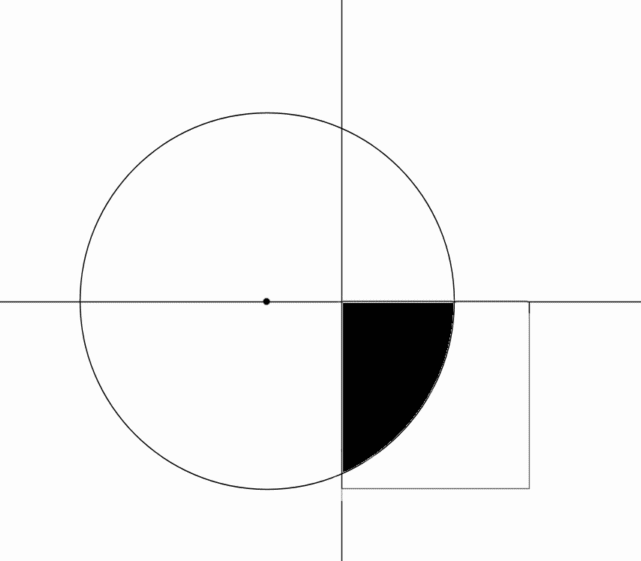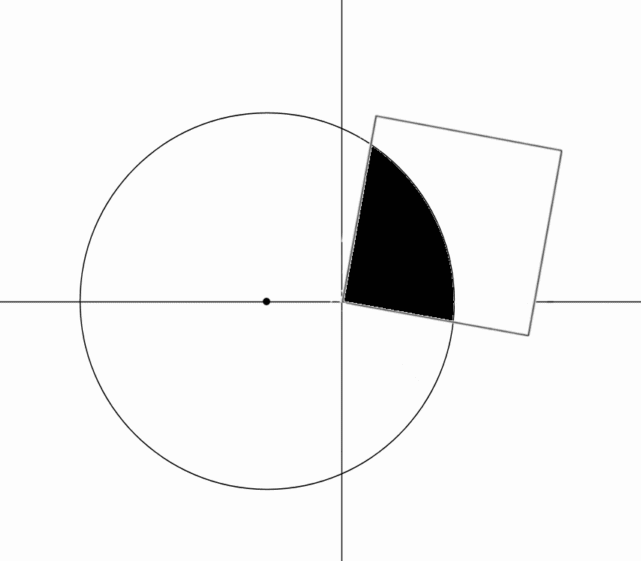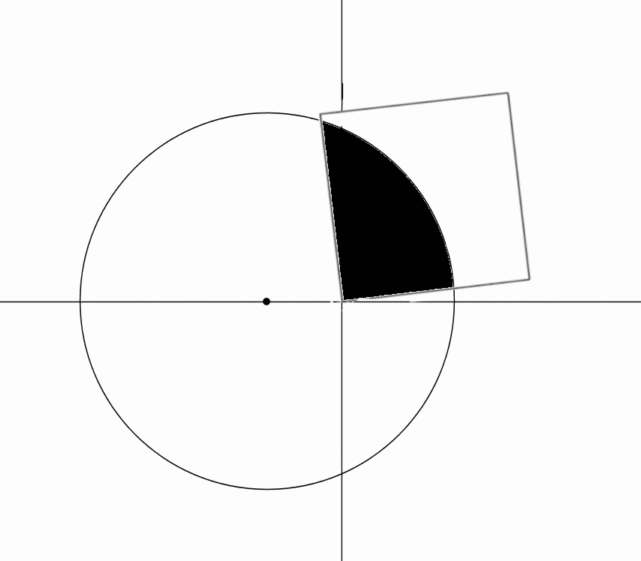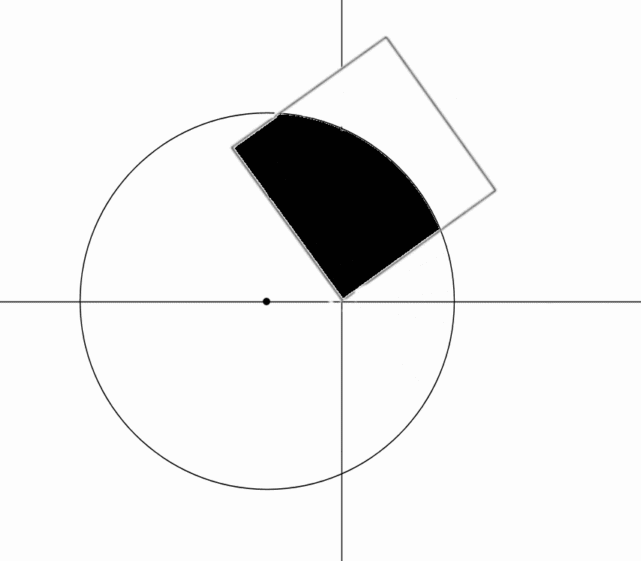 A square
is positioned in the
quadrant intersecting part of a circle of radius
and centered at
. The square is rotated counter-clockwise about the origin.
A square
is positioned in the
quadrant intersecting part of a circle of radius
and centered at
. The square is rotated counter-clockwise about the origin.
Through what angle (in degrees) does the square have to be rotated until of its area intersects with the circle?
[Answer to nearest 3 decimal places]
The answer is 110.146.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
To make the integration in this problem easier, we first rotate the origin O ( 0 , 0 ) clockwise about C ( − 2 , 0 ) by a variable angle θ . Its coordinates then become O ′ ( − 2 + 2 cos ( θ ) , − 2 sin ( θ ) ) . Now let O ′ serve as the lower left corner of a 5 by 5 square with sides that are parallel to the axes.
We will then integrate with respect to y while varying θ so that half the area of the square lies inside the circle. Once the necessary value for θ is found, we then rotate the square counterclockwise about C to get it into its "final" position. Now, relative to the initial position of the square as posed in the question, the angle the square will have been rotated about O to reach its "final" position is then ( 2 π + θ ) radians.
(Note: An assumption is being made that the top left corner of the square in its final position will lie inside the circle. This assumption was made after drawing a (rotated) square with its top left corner lying on the circle and then making a few quick calculations as to what fraction of the area a square with this orientation lay inside the circle. As this fraction was less than half, the above assumption was made. It is also clear visually that this is the case, and the following calculations will bear out this observation. Having this vertex lie inside the circle complicates the integration if done with respect to x , which is the motivation behind rotating O and performing the integration with respect to y .)
Now, integrating with respect to y , the equation for which we must solve for θ is
∫ − 2 sin ( θ 5 − 2 sin ( θ ) ( ( 2 5 − y 2 − 2 ) − ( − 2 + 2 cos ( θ ) ) ) d y = 2 2 5
⟹ ∫ − 2 sin ( θ ) 5 − 2 sin ( θ ) ( 2 5 − y 2 − 2 cos ( θ ) ) d y = 1 2 . 5 .
Now WolframAlpha could not solve this equation directly, so I had to enter in successive values for θ (in radians) until the integral returned a value of 1 2 . 5 . This was achieved after approximately ten iterations, resulting in a value for θ of 0 . 3 5 1 6 2 radians to 5 decimal places. Here is the final WA calculation.
(Note that the upper right corner of the square, (with the lower left corner at O ′ , for this value of θ will lie at ( − 0 . 1 2 2 3 6 8 , 4 . 3 1 1 1 6 2 ) , which lies below the "corresponding" point ( − 0 . 1 2 2 3 6 8 , 4 . 6 3 4 0 5 8 5 ) on the circle, thus confirming the observations made in the note above.)
The requested value for the angle of rotation, in degrees, is then
9 0 + ( π 1 8 0 ) ∗ 0 . 3 5 1 6 2 = 1 1 0 . 1 4 6 ∘ to 3 decimal places.