Twisted squares
The picture shows 4 nested squares, each rotated 30 degrees from the one touching it from inside.
If the outermost square has area 1, find the area of the innermost square, which can be written as A − B 3 .
Enter the value of A + B .
The answer is 328.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
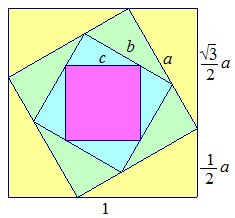Let the side length of the second outermost, second innermost and the innermost squares be
a
,
b
and
c
respectively. Then we note that
2
1
a
+
2
3
a
=
1
⟹
a
=
3
+
1
2
=
(
3
+
1
)
(
3
−
1
)
2
(
3
−
1
)
=
3
−
1
. Similarly,
b
=
(
3
−
1
)
a
=
(
3
−
1
)
2
and
c
=
(
3
−
1
)
3
. Then, the area of the innermost square
A
□
=
c
2
=
(
3
−
1
)
6
=
2
0
8
−
1
2
0
3
. Therefore,
A
+
B
=
2
0
8
+
1
2
0
=
3
2
8
.
Hi, can this be continued/extended to n such tilted squares to generalize? And also angles as well? It would be a fantastic discussion to see
Log in to reply
- I think for side n and angle θ , we will have the first equation as
- Then we rationalize to
a = sin ( θ ) + cos ( θ ) 1 × sin θ − cos ( θ ) sin θ − cos ( θ ) ⟹ a = sin 2 ( θ ) − cos 2 ( θ ) sin θ − cos ( θ )
- We continue to find the n th side to be
( sin 2 ( θ ) − cos 2 ( θ ) sin θ − cos ( θ ) ) n
My apologies for posting a problem nearly identical to yours. I thought I had created an original problem.
Log in to reply
No problem, it sometimes happens. Your followup is great by the way 👍
It's interesting to see how we draw the diagram. We think how big the square is, but in fact the area is just 0.1539. The scale is really off! By the way very nice problem. I had an extensions, can you please add on to my generalisation? Thanks
Log in to reply
- For side n and angle θ , we will have the first equation as
- Then we rationalize to
a = sin ( θ ) + cos ( θ ) 1 × sin θ − cos ( θ ) sin θ − cos ( θ ) ⟹ a = sin 2 ( θ ) − cos 2 ( θ ) sin θ − cos ( θ )
- We continue to find the n th side to be
( sin 2 ( θ ) − cos 2 ( θ ) sin θ − cos ( θ ) ) n
Let the shorter leg of the yellow right triangle be x , then the longer leg is 1 − x . Since this is a 30-60-90 right triangle, x 1 − x = 3 . Solving this gives x = 2 3 − 1 . The hypotenuse is twice this = 3 − 1 .
The side of each square is smaller than the one outside of it by this ratio. Since the largest has side 1 , the smallest has side ( 3 − 1 ) 3 = 6 3 − 1 0 and area ( 6 3 − 1 0 ) 2 = 2 0 8 − 1 2 0 3 . So A = 2 0 8 , B = 1 2 0 , A + B = 3 2 8