Twisting the Problem - "Complicated Tangency of a system of circles"!

Geometry Level 5

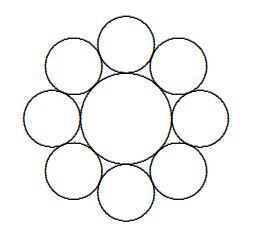Eight equal circles are mutually tangent in pairs and tangent externally to a unit circle as shown in the figure. If the common radius of the eight smaller circles can be expressed as:

A − B C − D − E \large{\dfrac{\sqrt{A-\sqrt{B}}}{C - \sqrt{D-\sqrt{E}}}}

for positive integers A , B , C , D , E A, B, C, D, E which doesn't have any square factor. Find the minimum value of A + B + C + D + E A+B+C+D+E .

Here is a senior version of this problem - Complicated Tangency of a system of Circles!


The answer is 10.

View wiki
Satyajit Mohanty by Satyajit Mohanty , 24, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

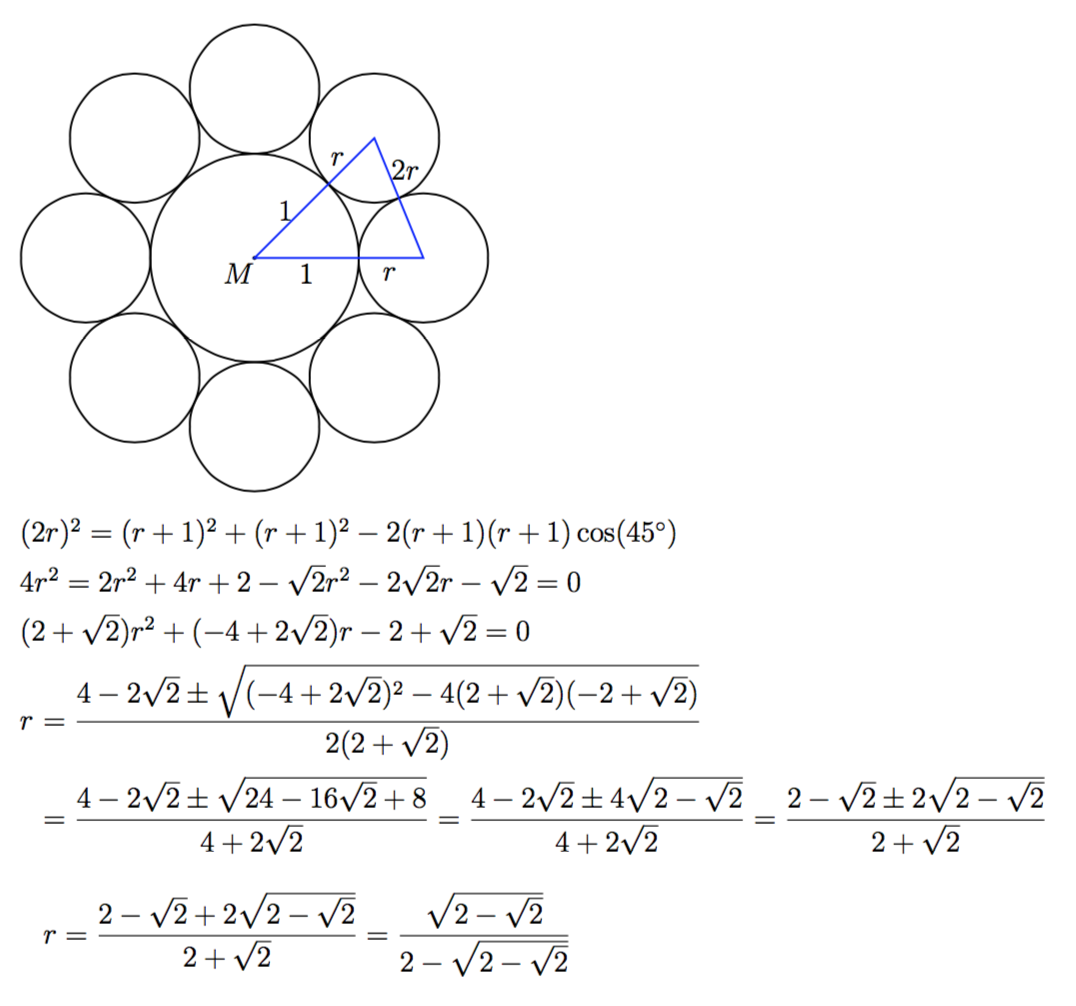
S i n 22. 5 o = 2 − 2 2 . For isosceles triangle, sides b, b, a and vertex angle A a 2 = b ∗ S i n A 2 . Triangle formed by centres of unit circle and two adjoining small circles with radii r, is isosceles, a = 2 r , b = 1 + r , A = 36 0 o 8 = 4 5 o . ∴ r = ( 1 + r ) ∗ S i n A 2 , ⟹ r = S i n 22. 5 o 1 − S i n 22. 5 o = 2 − 2 2 1 − 2 − 2 2 = 2 − 2 2 − 2 − 2 = A − B C − D − E A + B + C + D + E = 5 ∗ 2 = 10 Sin22.5^o=\dfrac{\sqrt{2-\sqrt2}} 2.\\ \text{For isosceles triangle, sides b, b, a and vertex angle A}\\ \dfrac a 2=b*Sin\dfrac A 2.\\ \text{Triangle formed by centres of unit circle and two adjoining small circles}\\ \text{with radii r, is isosceles, } a=2r, b=1+r, A=\dfrac{360^o} 8 =45^o.\\ \therefore~r=(1+r)*Sin\dfrac A 2,\\ \implies r=\dfrac{Sin22.5^o}{1-Sin22.5^o}=\large \dfrac{\frac{\sqrt{2-\sqrt2}} 2}{1-\frac{\sqrt{2-\sqrt2}} 2}\\ =\large \dfrac{\sqrt{2-\sqrt2}}{2-\sqrt{2-\sqrt2}}\\ =\large \dfrac{\sqrt{A-\sqrt B}}{C-\sqrt{D-\sqrt E}}\\ A+B+C+D+E=5*2=~~~~~~\Large \color{#D61F06}{10}

4 Helpful 0 Interesting 0 Brilliant 0 Confused

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...