Two adjacent circles
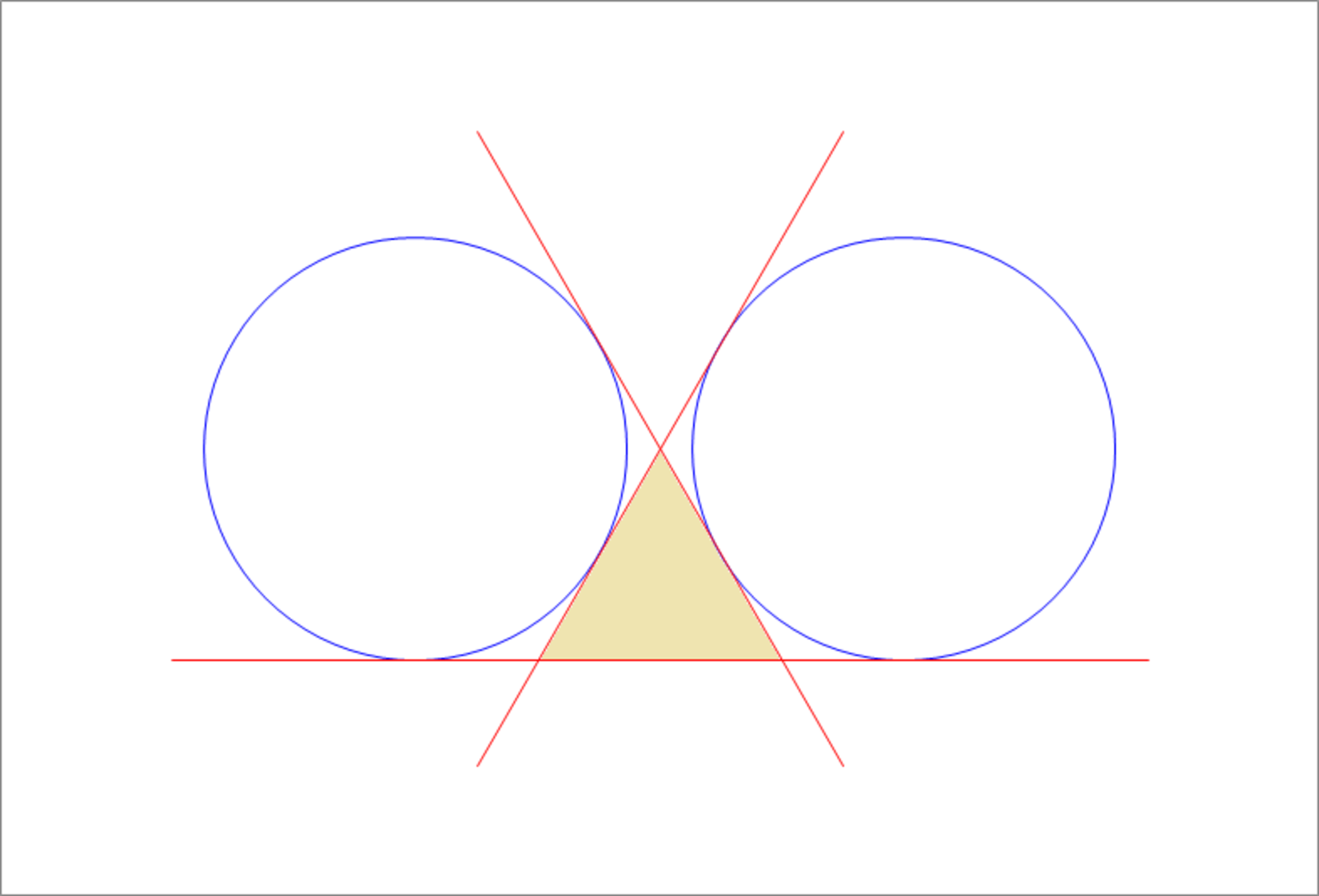
Two congruent adjacent circles of radius 1 0 have their centers lying on the x -axis and separated by a certain distance d such that the external common tangent to the circles from the bottom and the two internal common tangents form an equilateral triangle (shaded) as shown in the figure above. The area of the equilateral triangle can be expressed as b a , where a and b are positive integers and b is square-free. Find the product a b .
The answer is 300.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
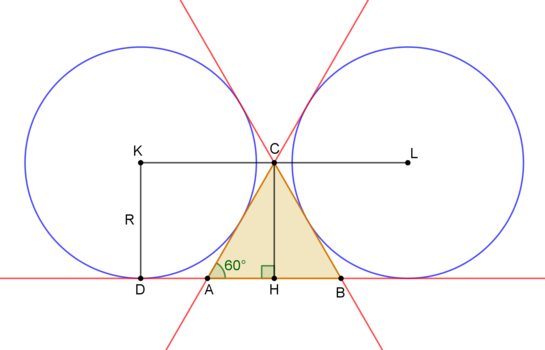 The line through the centers
K
and
L
of circles is parallel to the exterior tangent line and the point of intersection of the interior common tangent lines lies on
K
L
. Hence, the altitude
C
H
is congruent to the radius
K
D
, thus
C
H
=
1
0
.
Consequently, for the side
s
of the equilateral triangle we have
s
=
C
H
⋅
csc
6
0
∘
⇒
s
=
3
2
0
The area of the triangle is
4
s
2
3
=
3
1
0
0
For the answer,
a
=
1
0
0
,
b
=
3
, thus,
a
b
=
3
0
0
.
The line through the centers
K
and
L
of circles is parallel to the exterior tangent line and the point of intersection of the interior common tangent lines lies on
K
L
. Hence, the altitude
C
H
is congruent to the radius
K
D
, thus
C
H
=
1
0
.
Consequently, for the side
s
of the equilateral triangle we have
s
=
C
H
⋅
csc
6
0
∘
⇒
s
=
3
2
0
The area of the triangle is
4
s
2
3
=
3
1
0
0
For the answer,
a
=
1
0
0
,
b
=
3
, thus,
a
b
=
3
0
0
.
Each circle is an excircle of the equilateral triangle, which has a radius of r a = s − a s ( s − b ) ( s − c ) .
If each side of the equilateral triangle is x , then 1 0 = 2 3 x − x 2 3 x ( 2 3 x − x ) ( 2 3 x − x ) , which solves to x 2 = 3 4 0 0 .
Therefore, the area of the triangle is A = 4 3 x 2 = 4 3 ⋅ 3 4 0 0 = 3 1 0 0 , so a = 1 0 0 , b = 3 , and a b = 3 0 0 .
The radius is equal to the triangle's height if you rotate the 'hour hand' to 4.30 or 7.30. With 10 being its height, half of the base must be 1/√3 that, so area equal 10² x (1/√3) = 100/√3. Answer is 100 x 3 = 300.