Two adjacent incircles
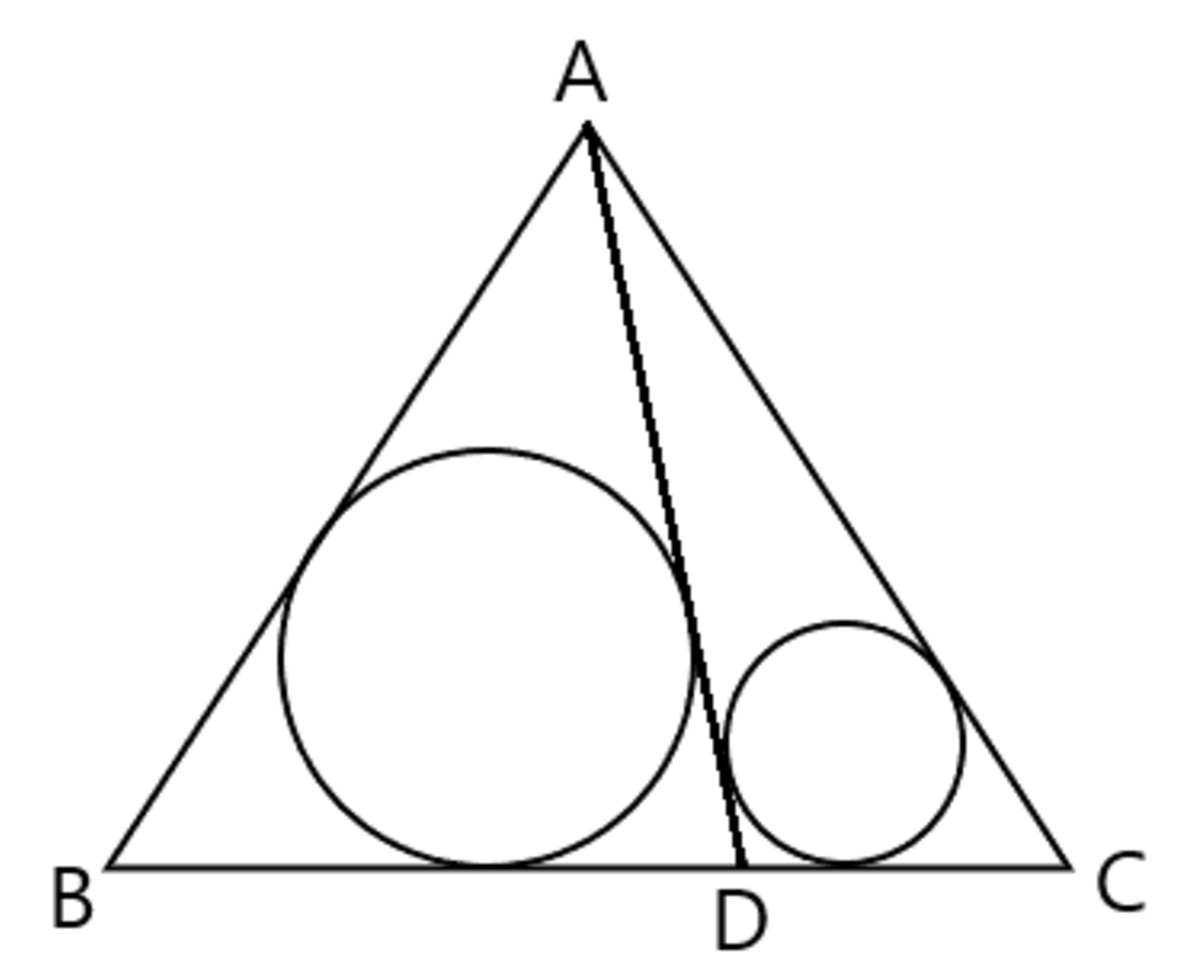
△ A B C is a unit equilateral triangle. Point D on B C is such that the inradius of △ A B D is twice the inradius of △ A D C . Find B D .
Diagram not drawn to scale
The answer is 0.70346.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
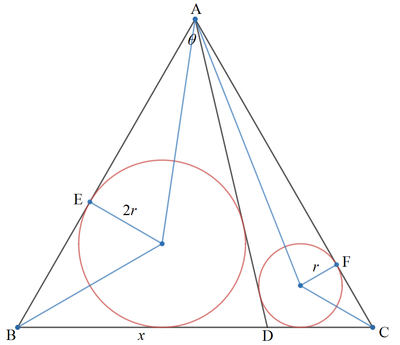
Let the tangent point of the big circle on A B and small circle on A C be E and F respectively, the radius of the smaller circle be r , and ∠ B A D = θ . Then
⎩ ⎪ ⎨ ⎪ ⎧ A E + E B = 2 r cot 2 θ + 2 r cot 3 0 ∘ = 1 A F + F C = r cot ( 3 0 ∘ − 2 θ ) + r cot 3 0 ∘ = 1 . . . ( 1 ) . . . ( 2 )
From ( 1 ) = ( 2 ) :
2 r cot 2 θ + 2 3 r t 2 + 3 ( 2 + 3 t ) ( 1 − 3 t ) 2 − 3 t − 3 t 2 4 t 2 + 2 3 t − 2 2 t 2 + 3 t − 1 ⟹ t = r tan ( 6 0 ∘ + 2 θ ) + 3 r = 1 − 3 t 3 + t = 3 t + t 2 = 3 t + t 2 = 0 = 0 = 4 1 1 − 3 Let t = tan 2 θ .
Let B D = x . By sine rule :
D C B D 1 − x x x ( 3 cos θ − sin θ ) x ( 3 cos θ + sin θ ) = sin ( 6 0 ∘ − θ ) sin θ = 2 3 cos θ − 2 1 sin θ sin θ = 2 sin θ − 2 x sin θ = 2 sin θ
⟹ x = 3 cos θ + sin θ 2 sin θ = 3 ( 1 − t 2 ) + 2 t 4 t = t 3 − 3 t + 2 4 = 1 1 − 3 4 3 − 4 3 3 − 3 + 2 4 = 4 2 3 3 + 6 − 4 3 3 − 3 + 2 4 = 3 3 + 1 7 1 6 = 1 6 1 7 − 3 3 ≈ 0 . 7 0 3
Another method consists in applying the formula for the distance d/d'from a vertex (B/C) to the incenter (I, for the big circle; I' for the small one) for triangles ABD and ADC. d=2d'. The general formula is: d(I,W)= sqr.((bc(p-w))/p), where "w" is the side of the triangle opposite to vertex W, "b" and "c" are the other two sides and "p" is de semiperimeter. We trace de height AH (= (sqr. 3)/2) of ABC, and cal "x" to the segment HD. By Pitagoras, AD, the common side to both triangles, is = sqr. (3/4+x^2). Introducing the data in the formulas it results that x=0.2, exactly. This means that for any side of the equilateral ABC the segment x= 1/5 of the side length.
Let B D = x and A D = y .
A triangle's inradius r , semiperimeter s and area T are related by T = r s
Here we have T A B D = r A B D s A B D and T A D C = r A D C s A D C
Dividing, T A D C T A B D = r A D C s A D C r A B D s A B D
Since Δ A B D and Δ A D C have the same height, the ratio of their areas is the ratio of their bases; so T A D C T A B D = D C B D = 1 − x x . Also, we're told r A B D = 2 r A D C , so that 1 − x x = 2 2 − x + y 1 + x + y
We can solve this for y to get y = 2 − 3 x x 2 + 2 x − 2
The cosine rule in Δ A B D gives y 2 = x 2 − x + 1
Combining these to eliminate y and rearranging, we get x ( x − 1 ) ( 8 x 2 − 1 7 x + 8 ) = 0
Solving this we find four roots for x ; three of these are outside the interval ( 0 , 1 ) , and are discarded; the other is x = 1 6 1 ( 1 7 − 3 3 ) ≈ 0 . 7 0 3 4 6