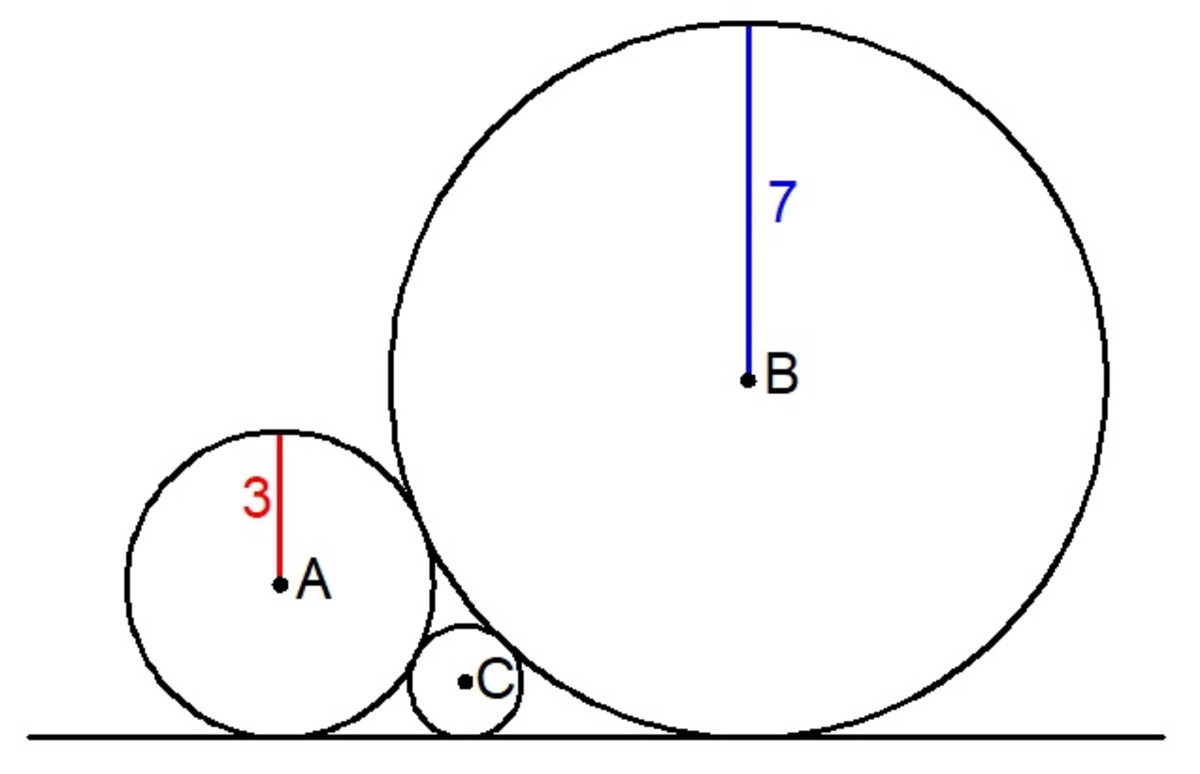
Two big circles and a small circle

Geometry Level 3

Three circles centered at $A,B$ and $C$ are tangent to each other and on a straight line as shown below. Given that the radii of the two bigger circles are $3$ and $7$ , respectively, find the radius of the smallest circle. If your answer can be expressed as $\dfrac{a-b\sqrt{b}}{c}$ where $a,b$ and $c$ are positive co-prime integers, give $a+b+c$ .

The answer is 134.

1 solution

Maria Kozlowska
Nov 26, 2017

Let $A', B', C'$ be corresponding points of tangency of three circles to the tangent line. Let $r$ be the radius of the smallest circle.

The length of the tangent segment for two externally tangent circles is a geometric mean of their diameters.

$A'B'=2 \sqrt{3 \times 7}$

$A'C'=2 \sqrt{3 \times r}$

$C'B'=2 \sqrt{r \times 7}$

$A'B'=A'C'+C'B' \Rightarrow 2 \sqrt{3 \times 7}=2 \sqrt{3 \times r}+2 \sqrt{r \times 7} \Rightarrow r=\dfrac{105-21\sqrt{21}}{8}$

Note: See also Tangent Circles