Two boys at the merry go round!
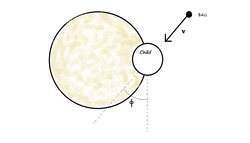 In Figure above, a
3
0
k
g
child stands on the edge of a stationary merry-go-round of radius
2
.
0
m
. The rotational inertia of the merry-go-round about its rotation axis is
1
5
0
k
g
m
2
• The child catches a ball of mass
1
.
0
k
g
thrown by a friend. Just before the ball is caught, it has a horizontal velocity
v
of magnitude
1
2
m
/
s
, at angle
ϕ
=
3
7
°
with. a line tangent to the outer edge of the merry-go-round, as shown. What is the angular speed (in rad/sec) of the merry-go-round just after the ball is caught?
In Figure above, a
3
0
k
g
child stands on the edge of a stationary merry-go-round of radius
2
.
0
m
. The rotational inertia of the merry-go-round about its rotation axis is
1
5
0
k
g
m
2
• The child catches a ball of mass
1
.
0
k
g
thrown by a friend. Just before the ball is caught, it has a horizontal velocity
v
of magnitude
1
2
m
/
s
, at angle
ϕ
=
3
7
°
with. a line tangent to the outer edge of the merry-go-round, as shown. What is the angular speed (in rad/sec) of the merry-go-round just after the ball is caught?
Liked it try some more
The answer is 0.070.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
In case of collisions it is better to talk in terms of angular impulse rather than torque.
How come it's a level 5 problem!!!!
Yes L = I ω = c o n s t a n t we have L i n i t i a l = ( m b a l l ) ( v c o s t h e t a ) ( R ) note v sin theta is irrelevant as it is along radius.And expression for I is I t o t a l = ( m b a l l + m c h i l d ) R 2 + I m e r r y g o r o u n d .There now we have all the information.just substitute to get ω .
AS NET TORQUE ABOUT THE CENTER OF MERRY GO ROUND IS ZERO WE CAN CONSERVE ANGULAR MOMENTUM ABOUT IT. m=mass of ball.
M=mass of child
r=radius of merry go round
L i = L f
m v r s i n ( 9 0 − ϕ ) = I ω
I = 1 5 0 + m r 2 + M r 2 = 2 7 4 k g − m 2
m v r sin ( 9 0 − ϕ ) = 1 × 1 2 × 2 s i n 5 3 = 1 9 . 2
19.2=274 ω
ω =0.070