Two charges at the ends of a rod .
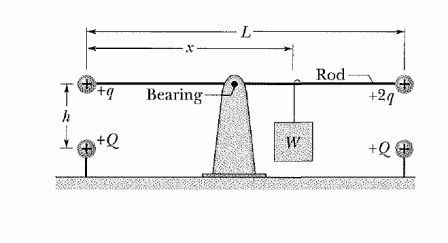The figure shows a long, nonconducting, massless rod of
length
, pivoted at its center and balanced with a block of weight
at a distance
from the left end. At the left and right ends of the rod
are attached small conducting spheres with positive charges
and
,
respectively. A distance h directly beneath each of these spheres is a
fixed sphere with positive charge
. The value
should have so that
the rod exerts no vertical force on the bearing when the rod is horizontal
and balanced can be expressed as
what is the value of
.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
all vertical forces are balanced so that the repulsive force(total) is equal to the weight of the block W=(1/4pi epsilon){3Qq/h^2}