Two Chords and an Angle
In a circle, chord A B and chord C D intersect at E such that A E = 4 , E B = 1 9 6 , D E = 1 4 , and ∠ C E B = cos − 1 ( − 1 7 8 ) .
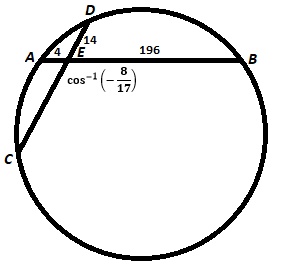
Find the radius of the circle.
The answer is 125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Fantastic solution!
Let F G be the perpendicular bisector of C D at G , let H I be the perpendicular bisector of A B at I , and let O be the intersection of F G and H I , and therefore the center of the circle.
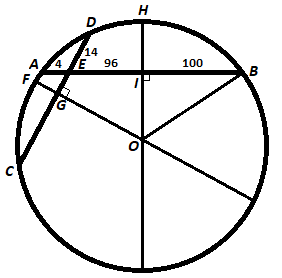
By the intersecting chords theorem , A E ⋅ E B = C E ⋅ E D , so 4 ⋅ 1 9 6 = C E ⋅ 1 4 , which means C E = 5 6 . Since I is a bisector of A B , I B = 1 0 0 and E I = 9 6 . Since G is a bisector of C D , C G = 3 5 and G E = 2 1 .
Let E be the origin and E B be the positive x -axis. Since ∠ C E B = cos − 1 ( − 1 7 8 ) , and ∠ A E G is supplementary to it, ∠ A E G = cos − 1 ( 1 7 8 ) . Since E G = 2 1 , it has an x -component of 2 1 cos ( cos − 1 ( 1 7 8 ) ) = 1 7 1 6 8 , and a y -component of 2 1 2 − ( 1 7 1 6 8 ) 2 = 1 7 3 1 5 , and so G has coordinates ( − 1 7 1 6 8 , − 1 7 3 1 5 ) .
Chord C D has a slope of tan ( cos − 1 ( 1 7 8 ) ) = 8 1 7 2 − 8 2 = 8 1 5 , and since F G is perpendicular to C D , F G has a slope of − 1 5 8 , and therefore an equation of y + 1 7 3 1 5 = − 1 5 8 ( x + 1 7 1 6 8 ) .
Since H I is perpendicular to the x -axis, and E I = 9 6 , H I is a vertical line with an equation of x = 9 6 .
Therefore, since O is the intersection of F G and H I , its coordinates are the solution to y + 1 7 3 1 5 = − 1 5 8 ( x + 1 7 1 6 8 ) and x = 9 6 , which is ( 9 6 , − 7 5 ) , which means I O = 7 5 .
Finally, by Pythagorean's Theorem on △ O H B , the radius O B = I O 2 + I B 2 = 7 5 2 + 1 0 0 2 = 1 2 5 .
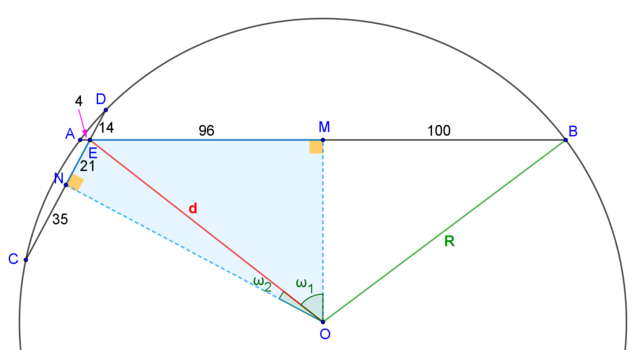 Let
O
be the center of the circle,
M
,
N
the midpoints of
A
B
and
C
D
respectively.
Then
O
M
⊥
A
B
and
O
N
⊥
C
D
, so
∠
O
N
E
+
∠
O
M
E
=
π
. Hence
O
M
E
N
is a cyclic quadrilateral. Consequently,
∠
M
E
N
+
∠
M
O
N
=
π
⇒
cos
(
M
O
N
)
=
−
cos
(
M
E
N
)
⇒
cos
(
M
O
N
)
=
1
7
8
Let
O
be the center of the circle,
M
,
N
the midpoints of
A
B
and
C
D
respectively.
Then
O
M
⊥
A
B
and
O
N
⊥
C
D
, so
∠
O
N
E
+
∠
O
M
E
=
π
. Hence
O
M
E
N
is a cyclic quadrilateral. Consequently,
∠
M
E
N
+
∠
M
O
N
=
π
⇒
cos
(
M
O
N
)
=
−
cos
(
M
E
N
)
⇒
cos
(
M
O
N
)
=
1
7
8
By the
intersecting chords theorem
, same way as @David Vreken did, we have
A
E
⋅
E
B
=
C
E
⋅
E
D
, so
4
⋅
1
9
6
=
C
E
⋅
1
4
, thus,
C
E
=
5
6
.
Since
M
and
N
are midpoints, we get
E
M
=
9
6
,
M
B
=
1
0
0
,
C
N
=
3
5
,
N
E
=
2
1
.
Let ∠ M O E = ω 1 , ∠ N O E = ω 2 , O B = R and O E = d . Then, sin ω 1 = d 9 6 , sin ω 2 = d 2 1 , cos ω 1 = 1 − ( d 9 6 ) 2 and cos ω 2 = 1 − ( d 2 1 ) 2 .
Now, we have an equation for d :
cos ( ∠ M O N ) = cos ( ω 1 + ω 2 ) ⇔ 1 7 8 = cos ω 1 ⋅ cos ω 2 − sin ω 1 ⋅ sin ω 2 ⇔ 1 7 8 = 1 − ( d 9 6 ) 2 ⋅ 1 − ( d 2 1 ) 2 − d 9 6 ⋅ d 2 1 ⇔ ⋯ ⇔ d 2 = 1 4 8 4 1
Finally comes Pythagorean Theorem:
O B 2 = M B 2 + O M 2 ⇒ R 2 = 1 0 0 2 + ( d 2 − E M 2 ) ⇒ R 2 = 1 0 0 2 + ( 1 4 8 4 1 − 9 6 2 ) ⇒ R = 1 2 5
Great solution!
Fantastic solution!
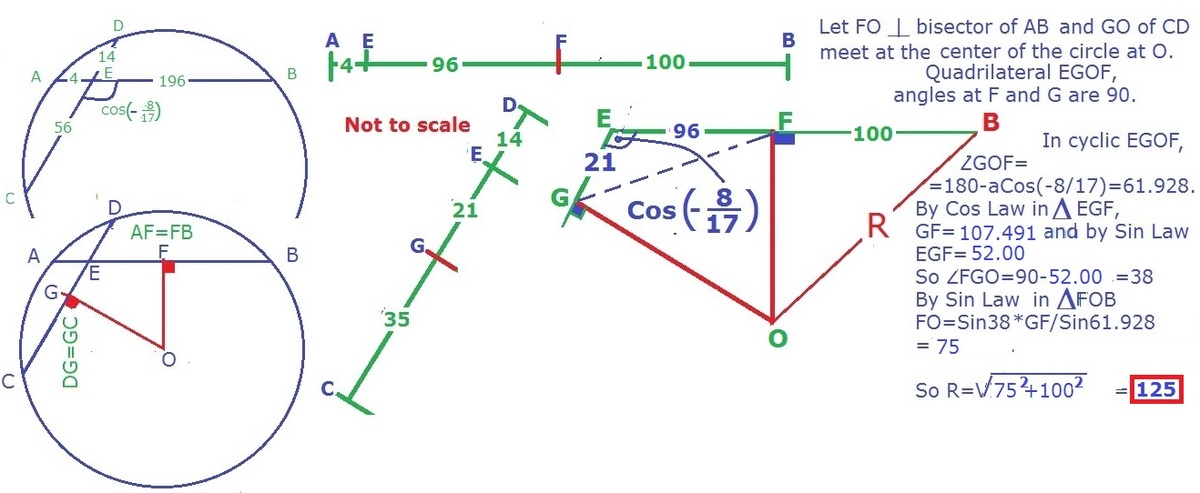
the first thing to do is to find DB. then using a combination of law of sine and cosine find sin θ , and end it by using 2 r sin θ = D B .notice inscribed angle theorem was used. first D B 2 = 1 4 2 + 1 9 6 2 − 2 1 7 8 ∗ 1 4 ∗ 1 9 6 → D B = 3 5 0 1 7 5 then B C 2 = 5 6 2 + 1 9 6 2 + 2 1 7 8 ∗ 5 6 ∗ 1 9 6 → B C = 4 2 0 1 7 5 and by laws of sine sin θ 1 9 6 = sin ( arccos ( − 8 / 1 7 ) ) 4 2 0 1 7 5 → sin θ 1 = 7 1 7 1 7 5 this gives r = 2 sin θ D B = 2 1 × 3 5 0 1 7 5 × 7 1 7 1 7 5 = 1 2 5