Two Circles and a Square: Find the area of the square
In the figure shown below, the blue line is 8 units long and the red line is 12 units long. Find the area of the square in square units.
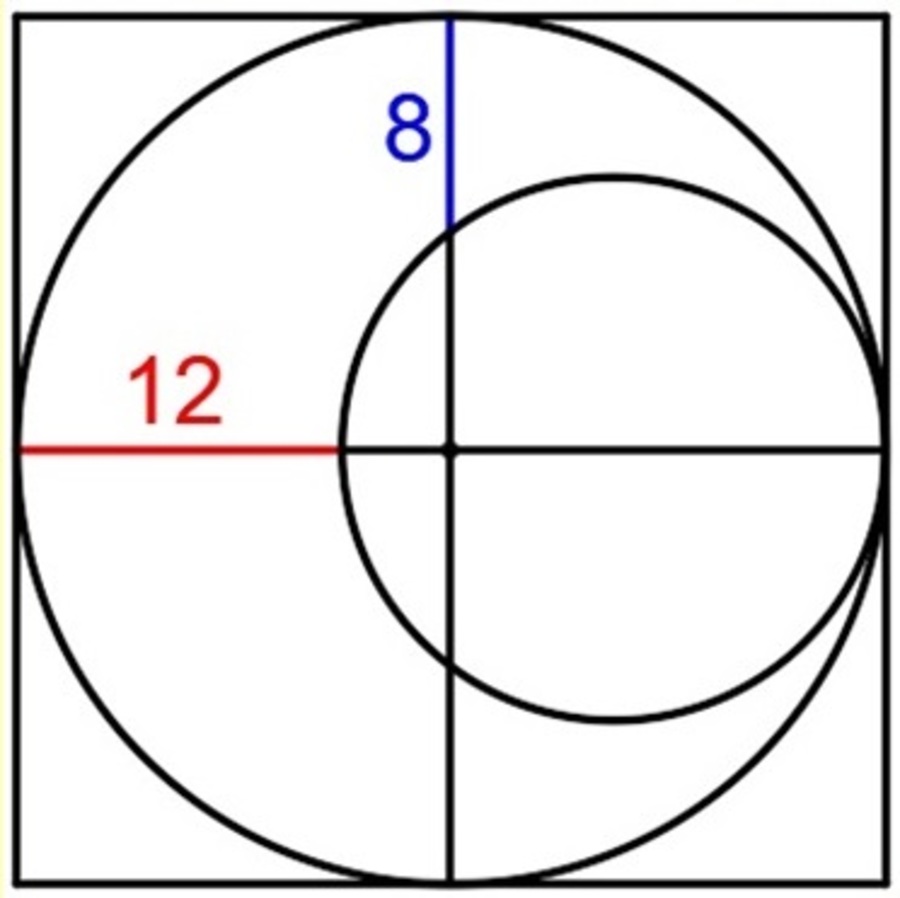 .
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Coordinate geometry seems the easiest way to go: put an origin at the centre of the diagram, and let the large circle have radius R and the small one radius r . From the diagram, the centre of the smaller circle is at ( R − r , 0 ) so its equation is ( x − R + r ) 2 + y 2 = r 2 .
This circle intersects the negative x -axis at ( R − 2 r , 0 ) , so that R − 2 r = − R + 1 2
At the intersection with the positive y -axis we have ( R − r ) 2 + ( R − 8 ) 2 = r 2
From the first equation, we get R − r = 6 . The second equation then becomes 6 2 + ( R − 8 ) 2 = r 2
Rearranging, we have R 2 − r 2 = 1 6 R − 1 0 0
Dividing by R − r = 6 gives R + r = 6 1 ( 1 6 R − 1 0 0 )
Adding R − r = 6 again we get 2 R = 6 + 6 1 ( 1 6 R − 1 0 0 )
which is easily solved to find R = 1 6 , so the side of the square is 3 2 and its area is 1 0 2 4 .
I think geometric way is better though
Log in to reply
Agreed - but not when you're trying to draw a diagram on a phone! The purely geometric ways I tried (intersecting chords/power of a point) ultimately led to the same equations. Did you find any shortcuts?
Let radius of larger circle
=
R
, radius of smaller circle
=
r
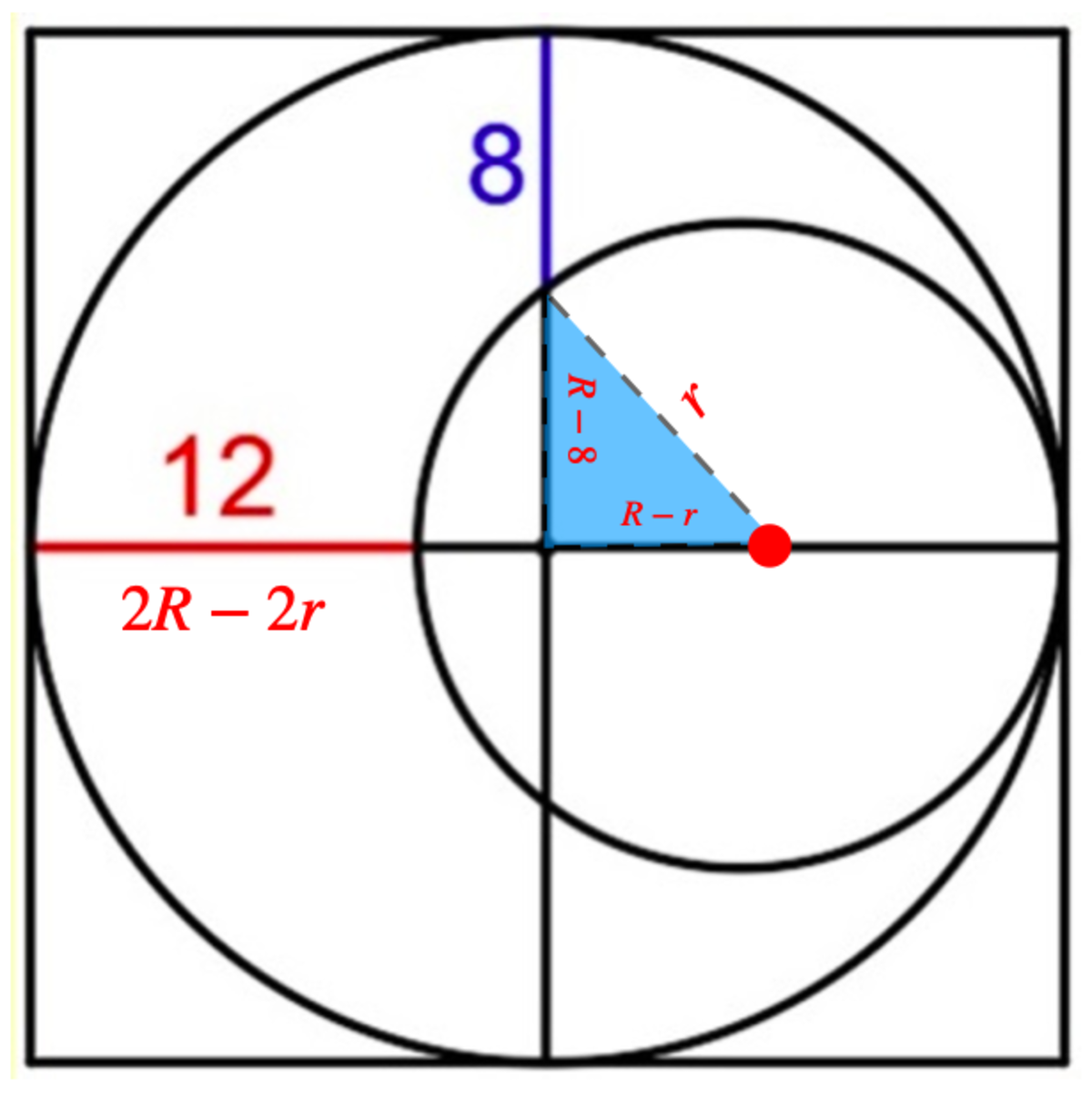
2 R − 2 r ⟹ R ( R − r ) 2 + ( R − 8 ) 2 6 2 + ( r − 2 ) 2 r ⟹ R = 1 2 = r + 6 = r 2 = r 2 = 1 0 = 1 6
Side of the square = 2 R = 3 2 . Area of square = 3 2 2 = 1 0 2 4
Let the quarter's side length be x+12, then the right triangle inside the smaller circle will have a height of x+4 (that's x+12-8) with a left base x and a right base x+12. Using similar right triangle,
x/(x+4) = (x+4)/(x+12).
x(x+12) = (x+4)².
x = 4.
Answer.
= [2(x+12)]².
= 1024
Let the side length of the square be 2 a . Consider the two intersecting chords in the smaller circle. By intersecting chords theorem ,
( a − 1 2 ) a a 2 − 1 2 a 4 a a = ( a − 8 ) 2 = a 2 − 1 6 a + 6 4 = 6 4 = 1 6
Therefore, the area of the square is ( 2 a ) 2 = 1 0 2 4 .