Two Circles and a Square
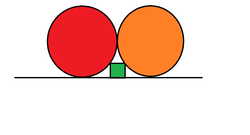 Two identical touching circles of radius
share the same tangent.
A square of side
, rests on the tangent and touches the two circles as shown in the diagram above.
Two identical touching circles of radius
share the same tangent.
A square of side
, rests on the tangent and touches the two circles as shown in the diagram above.
If is 10 units. Then the side of the square is how many units?
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
From the figure shown, form the equation using pythagoras theorem,
2r = 2*sqrt(r^2 - (r-s)^2) + s
Solve the quadratic, for r, which will give you two solutions.
Only one of them is valid which yields s = 0.4*r