Two Circles in a Triangle

Let $R=6762$ , $r=3450$ , and the smallest angle of the right triangle be $\theta$ . Then the base of the triangle is $b=\dfrac R{\tan \frac \theta 2} + R$ , the height of the triangle is $h = b \tan \theta$ , and the area of the triangle is $A = \dfrac {bh}2$ . Since $R$ is the inradius of the triangle, $A= \frac {Rp}2$ , where $p$ is the perimeter of the triangle. Then we have:

$\begin{aligned} \frac {Rp}2 & = \frac 12 \left(\frac R{\tan \frac \theta 2}+R\right)^2 \tan \theta & \small \blue{\text{Let }t=\tan \frac \theta 2} \\ \implies p & = R \left(\frac 1t + 1\right)^2 \times \frac {2t}{1-t^2} = \frac {2R(1+t)}{t(1-t)} \end{aligned}$

To find $t = \tan \frac \theta 2$ , we let the distance between the left vertex to the center of the small circle be $x$ . Then by similar triangles we have:

$\begin{aligned} \frac xr & = \frac {x+r+R}R \\ Rx & = rx + r^2 + rR \\ \implies x & = \frac {r(R+r)}{R-r} = 10637.5 \\ \implies t & = \tan \frac \theta 2 = \frac r{\sqrt{x^2-r^2}} = \frac {12}{35} \end{aligned}$

Therefore $p = \dfrac {2R(1+t)}{t(1-t)} = \boxed{80605}$

Put an origin at the right-angle. Let the two vertices of the triangle on the $x$ -axis be $(0,0)$ and $(a,0)$ , and the vertex on the $y$ -axis be $(0,b)$ , so the sides of the triangle are $a$ , $b$ and $c=\sqrt{a^2+b^2}$ .

The incircle has centre $(6762,6762)$ ; the smaller circle has centre $(u,3450)$ . The distance between their centres is the sum of their radii; so $(u-6762)^2+(6762-3450)^2=(6762+3450)^2$

Solving, $u=16422$ .

The centres and the point $(a,0)$ form a straight line. Equating gradients (or rather, their reciprocals, to get a nicer equation), $\frac{a-16422}{3450} = \frac{a-6762}{6762}$

Solving, $a=\frac{52969}{2}$

The inradius of a right-angled triangle is given by $\frac12 (a+b-c)$ ; we also have $a^2+b^2=c^2$ . Putting these together and solving, we find $b=20580$ and $c=\frac{67081}{2}$ , so the perimeter of the triangle is $\boxed{80605}$ .

Let $R = 6762$ , $r = 3450$ , $D$ , $E$ , $F$ , $G$ , $H$ points of tangency of the sides of the triangle with the circles, $K$ , $L$ the centers of the circles, $CE = CF = x$ ,
$BG = BH = y$ (tangent lines to the circles), $LM \bot KD$ .

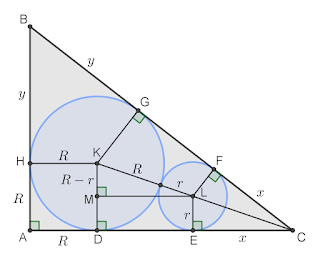
By Pythagoras theorem on $\vartriangle KLM$ , $LM = \sqrt {{{\left( {R + r} \right)}^2} - {{\left( {R - r} \right)}^2}} = 2\sqrt {Rr} = 9660,$ hence, $DE = FG = LM = 9660$ .

The points $K$ and $L$ lie on the angle bisector of $\angle ACB$ and by similarity of $\vartriangle CLE$ and $\vartriangle CKD$ , $\frac{x}{r} = \frac{{x + 9660}}{R}$ which solves to $x = 10062.5$ .

Again by Pythagoras theorem, this time on $\vartriangle ABC$ , ${\left( {y + 9660 + x} \right)^2} = {\left( {y + R} \right)^2} + {\left( {R + 9660 + x} \right)^2}$ which solves to $y = 13818$ .

Finally, for the perimeter $P$ of $\vartriangle ABC$ we have $P = 2\left( {x + y + R + 9660} \right) =\boxed{80605}$ .

The base of the triangle has length $b=6762+\sqrt {(6762+3450)^2-(6762-3450)^2}(1+\dfrac{3450}{3312})=26484.5$ . Let the triangle be $\triangle {ABC}$ right angled at $C$ and base $\overline {CA}$ . Then $\sin (\dfrac{A}{2})=\dfrac{3312}{10212}$ . This gives $\tan A=\dfrac{840}{1081}$ . So $a=|\overline {BC}|=b\tan A=20580$ and $c=|\overline {AB}|=\sqrt {a^2+b^2}=33504.5$ . Therefore the perimeter of the triangle is $26484.5+20580+33504.5=\boxed {80605}$