Two Circles touching each other

Let $AB$ and $PQ$ meet in point $D$ , let $AD=b$ and $DQ=a$ . Now $\triangle ADQ$ and $\triangle ADP$ are identical right angled triangles. Their combined area equals $ab=\frac{9\sqrt{3}}{4}$ The rest of the solution is given below

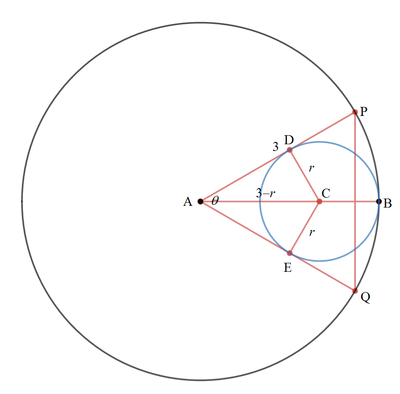
Let the center of the small circle be $C$ , its radius $r$ , the tangent points of $AP$ and $AQ$ be $D$ and $E$ respectively, and $\angle PAQ = \theta$ . Then the area of $\triangle APQ$ :

$\begin{aligned} [APQ] & = \frac {AP \cdot AQ \cdot \sin \angle PAQ}2 \\ & = \frac {3\cdot 3\sin \theta}2 = 9 \sin \frac \theta 2 \cos \frac \theta 2 & \small \blue{\text{Note that }\sin \frac \theta 2 = \frac r{3-r}} \\ & = \frac {9r\sqrt{(3-r)^2-r^2}}{(3-r)^2} & \small \blue{\text{Putting }[APQ] = \frac {9\sqrt 3}4} \\ \sqrt 3 (3-r)^2 & = 4r\sqrt{(3-r)^2-r^2} & \small \blue{\text{Squaring both sides.}} \\ 3r^4 - 36r^3 + 162r^2 - 324r + 243 & = 144r^2 - 96r^3 \\ 3r^4 + 60 r^3 + 18r^2 - 324r + 243 & = 0 \\ r^4 + 20 r^3 + 6r^2 - 108r + 81 & = 0 \\ (r-1)(r+3)(r^2 + 18r -27) & = 0 \\ \implies r & = 1, -3, \pm 6\sqrt 3 - 9 \end{aligned}$

Since $r > 0$ , the sum of all possible values of $r$ is $1 + 6\sqrt 3 - 9 = 6\sqrt 3 - 8$ and the required answer is $\boxed 3$ .