Two dice sets

Probability Level 4

Bob and Alice are playing a dice game. The dice is rolled and Bob writes down a number in his notebook, if it has not already been written down. If the dropped out dice number is already written in Bob's notebook and Alice does not have it, then Alice writes this number in her notebook. The game ends when Bob has all the numbers $1,2,3,4,5,6$ written down in his notebook. If the expected value of the quantity of numbers in Alice's notebook in the game is $\frac AB$ , where $A,B$ are coprime positive integers, submit your answer as $A+B$ .

Bob wins if size Alice's set is 5, Alice wins if size Alice's set is 4. Otherwise, the prize goes to charity.

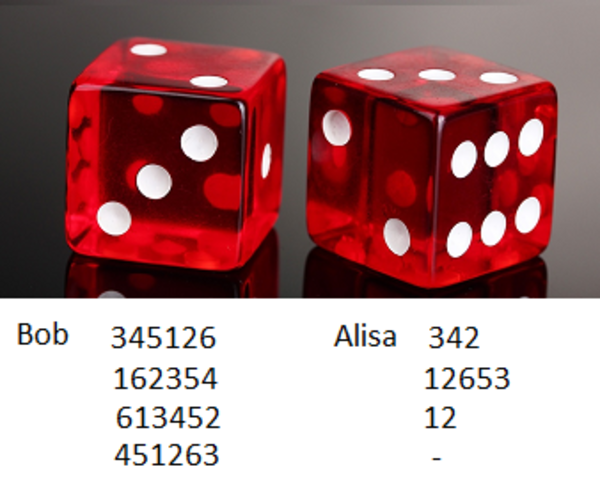
Example. Dice set $1,3,4,1,4,5,2,2,5,5,4,6$ , Bob set - $1,3,4,5,2,6$ , Alice set - $1,4,2,5$ - and the quantity of numbers $4$ .

The answer is 91.

3 solutions

Mark Hennings
Oct 4, 2020

Let $E_{b,a}$ be the expected number of numbers in Alice's final list, given that Bob currently has $b$ numbers in his list, and Alice has $a$ of them, for $0 \le a \le b \le 6$ , excluding the case $a=b=6$ . We can define the following recursive relations: $\begin{array}{rclcll} E_{6,a} & = & a & \hspace{1cm} & 0 \le a \le 5 \\ E_{b,b} & = & E_{b+1,b} & & 0 \le b \le 5 \\ E_{b,a} & = & \tfrac{b-a}{6}E_{b,a+1} + \tfrac{b}{6}E_{b,a} +\tfrac{6-b}{6}E_{b+1,a} & & 0 \le a < b < 6 \end{array}$ and these equations give $E_{0,0} = \tfrac{71}{20}$ , making the answer $71+20=\boxed{91}$ .

Thanks for attention.

Yuriy Kazakov - 8 months, 1 week ago

I'm sorry but I can't quite understand how you got the E(0,0) = 71/20

Aatmoshru Goswami - 8 months, 1 week ago

$E_{0,0}$ can be expressed in terms of $E_{1,0}$ and $(E_{0,1}$ , $E_{1,0}$ can be expressed in terms of $E_{2,0}$ and $E_{1,1}$ and so on. The above relations, used many times, express $E_{0,0}$ in terms of $E_{6,a}$ for $0 \le a \le 5$ , and hence we can calculate $E_{0,0}$ .

Mark Hennings - 8 months, 1 week ago

Hello Sir , can you suggest me a good Maths book equivalent to the Feynmen lectures on Physics?

kal kal - 8 months, 1 week ago

Patrick Corn
Oct 5, 2020

Set $a$ to be the number of numbers Alice has not written yet, and $b$ to be the number of numbers Bob has not written yet. The following Python program computes $E(6,6) = \frac{71}{20}.$

from fractions import Fraction
def E(a,b):
   if b == 0:
      return 6-a
   if a == b:
      return E(a,b-1)
   return Fraction(b,a)*E(a,b-1) + Fraction(a-b,a)*E(a-1,b)

Yuriy Kazakov
Oct 4, 2020

Absorbing Markov chain give probability $P(k)$ for length $k$ of Alisa final list. Excel use to calculate inverse matrix and matrix product.

$P(0)=\frac{5}{324}$

$P(1)=\frac{12281}{202500}$

$P(2)=\frac{218893}{1620000}$

$P(3)=\frac{356933}{1620000}$

$P(4)=\frac{460463}{1620000}$

$P(5)=\frac{460463}{1620000}$

Checking

$\frac{5}{324}+\frac{12281}{202500}+\frac{218893}{1620000}+\frac{356933}{1620000}+\frac{460463}{1620000}+\frac{460463}{1620000}=1$

Calculate the expected number

$\sum_{k=0}^{k=5} kP(k)=0\cdot \frac{5}{324}+1\cdot \frac{12281}{202500}+2\cdot \frac{218893}{1620000}+3\cdot \frac{356933}{1620000}+4\cdot \frac{460463}{1620000}+5\cdot \frac{460463}{1620000}=\frac{71}{20}$

Yuriy Kazakov - 8 months, 1 week ago

Fun fact: the $27$ possible states (Bob, Alice pairs) are all the tiles in a standard set of dominos except the double six.

Chris Lewis - 8 months, 1 week ago

Two dice sets

The answer is 91.

3 solutions

0 pending reports