Two Different Things

Electricity and Magnetism Level 1

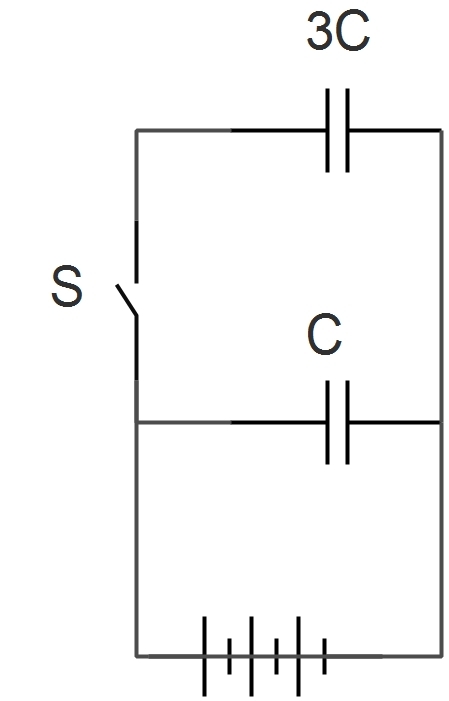
Two identical parallel plate capacitors are connected to a battery with the switch S S closed. When S S is opened and the free space between the capacitors is filled with a material of dielectric constant K K , the ratio of the total electrostatic energies stored in both capacitors, after and before the introduction of the dielectric, is __________ \text{\_\_\_\_\_\_\_\_\_\_} .

1 4 ( K + 3 K ) \dfrac{1}{4}\left(K+\frac{3}{K}\right) 1 6 ( K + 3 2 K ) \dfrac{1}{6}\left(K+\frac{3}{2K}\right) 1 2 ( K + 6 K ) \dfrac{1}{2}\left(K+\frac{6}{K}\right) 1 4 ( K + 4 5 K ) \dfrac{1}{4}\left(K+\frac{4}{5K}\right)

Rohit Ner by Rohit Ner , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Parth Sankhe
Oct 12, 2018

Energy before dielectric = 1 2 ( C + 3 C ) V 2 \frac {1}{2} (C+3C)V^2

After S is closed, the charge on the upper capacitor will be conserved(as it is no longer connected to a battery), while the voltage on the lower one will be conserved(as it will still be connected to the battery).

Q 1 = 3 C V = c o n s t a n t Q_{1}=3CV=constant

(As the dielectric is introduced, the capacitance of each capacitor gets multiplied by it's directric constant)

New energy in the upper capacitor = Q 1 2 2 C 1 = 9 C 2 V 2 2 ( 3 K C ) = 3 C V 2 2 K \frac {Q_{1}^2}{2C_{1}}=\frac {9C^2V^2}{2(3KC)}=\frac {3CV^2}{2K}

New energy in the lower capacitor = 1 2 ( K C ) V 2 \frac {1}{2}(KC)V^{2}

Adding the new energies and dividing by the original energy, we have the answer.

7 Helpful 0 Interesting 0 Brilliant 2 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...