Two Dimensional Collision
Two discs, each of radius 2 cm , the first of mass m 1 = 1 0 0 grams (shown in red), and the second of mass m 2 = 2 0 0 grams (shown in green) are on the horizontal x y plane, such that the initial position (at t = 0 ) of the center of the first disc is at ( − 1 0 , − 8 ) cm , and the initial position of the center of the second disc is at ( 0 , − 7 ) cm . They are moving with constant velocities. The velocity of the red disc is ( 0 . 5 , 0 . 4 ) cm/sec , and the velocity of the green disc is ( 0 . 1 , 0 . 3 ) cm/sec . The two discs undergo a perfectly elastic collision, where the total kinetic energy of the two discs is conserved, in addition to the conservation of the total linear momentum. Find the time instant (in seconds) when the green disc completely crosses the line y = 1 2 cm . If that time instant is T , then enter ⌊ 1 0 0 0 T ⌋ as your answer.
For more information about two-dimensional collision, you can read this wiki
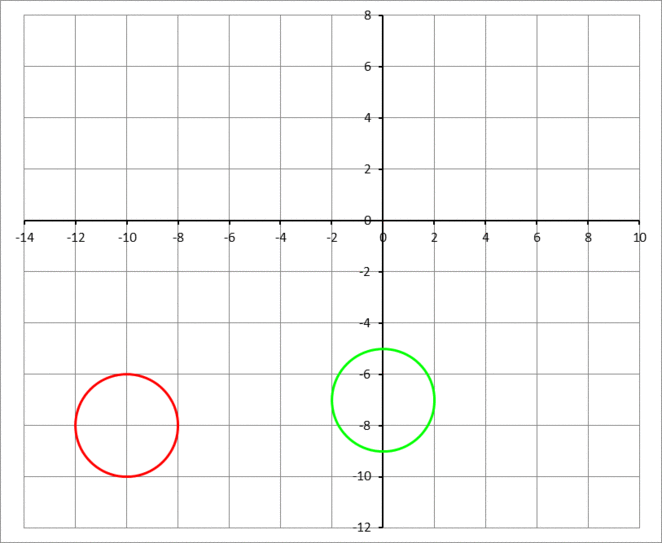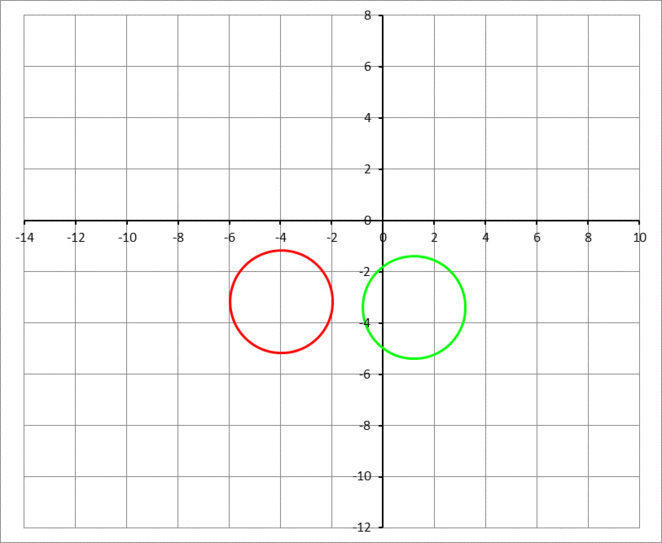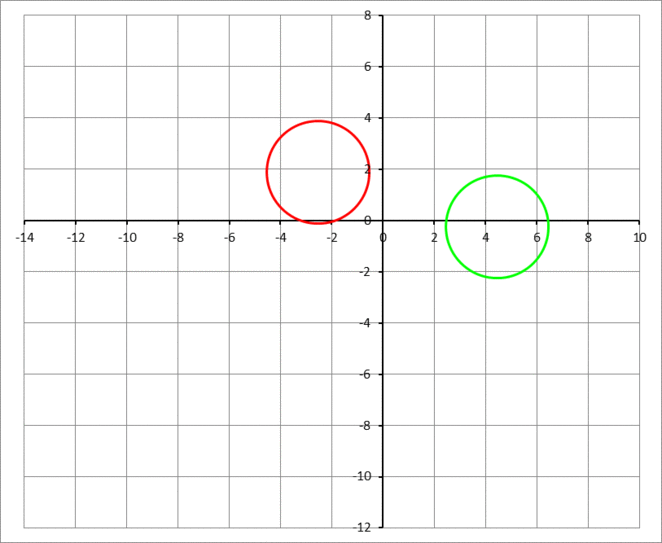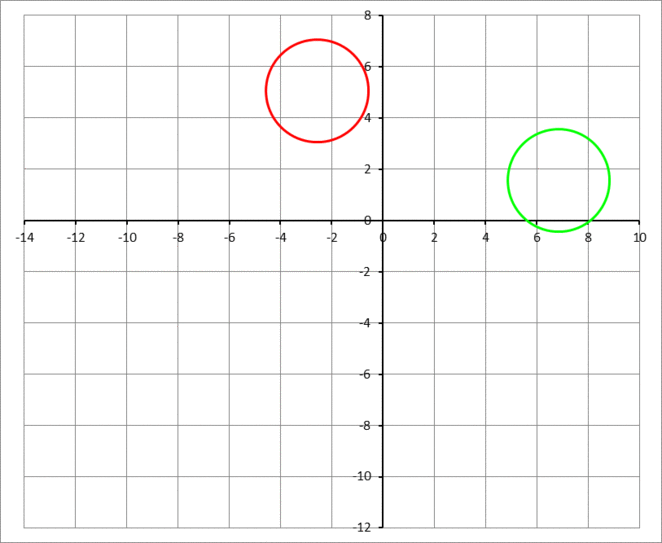
The answer is 76677.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
But how can you determine the point of collision? I thought the hardest part of this problem was to finding that point, cause afterwards total T can calculated with momentum or energy formulas. Are there any mathematical approach to finding it without using animation?
Log in to reply
One could write equations to solve, but using a computer program and sweeping the time/position was much easier for me
Note: since nothing was said about friction coefficients, or moments of inertia, we will have to make the assumption that the forces are central, i.e. disks are not exchanging angular momentum. For a high-accuracy calculation that should be noted.
There are four scalar quantities that are conserved:
- momentum in the x-direction: m 1 v 1 , x + m 2 v 2 , x
- momentum in the y-direction: m 1 v 1 , y + m 2 v 2 , y
- kinetic energy : 2 1 m 1 ( v 1 , x 2 + v 1 , y 2 ) + 2 1 m 2 ( v 2 , x 2 + v 2 , y 2 )
- angular momentum : m 1 ( x 1 v 1 , y − y 1 v 1 , x ) + m 2 ( x 2 v 2 , y − y 2 v 2 , x ) .
At the instant of collision, we expect two solutions for the set of four variables ( v 1 , x , v 1 , y , v 2 , x , v 2 , y ) , of which one represents the velocities before, and the other the velocities after collision.
To simplify the math somewhat, we switch to the reference frame that moves along with the centre of mass, and we will use vector notation and use momentum p = m v . This will make things much easier for us, because in that frame the conservation laws simplify to:
- momentum: p 2 = − p 1 so that
- kinetic energy: 2 m 1 1 p 1 2 + 2 m 2 1 p 2 2 is conserved ⇔ ∣ p 1 ∣ is conserved
- angular momentum: x 1 × p 1 + x 2 × p 2 = ( x 1 − x 2 ) × p 1 is conserved
So in this frame both the length of p 1 and its outer product with the connection line between the centres of the disks are conserved. This is consistent with our assumption of a central force: momentum is exchanged along the connection line.
The centre of mass moves as C M = ( 3 0 − 1 0 0 + 7 t , 3 0 − 2 2 0 + 1 0 t )
Relative to the c.o.m. we have x 1 = ( 3 0 − 2 0 0 + 8 t , 3 0 − 2 0 + 2 t ) and x 2 = ( 3 0 1 0 0 − 4 t , 3 0 1 0 − t )
so that, before collision p 1 = m 1 v 1 = ( 3 8 0 , 3 2 0 ) and ∣ p 1 ∣ = 2 7 . 4 8 7 3 7
In order to find the location of collision, we need to find the instant of collision, the lowest solution of ∣ x 1 − x 2 ∣ = 4 . We find t c o l l i s i o n = 2 × 0 . 1 7 8 . 2 − 8 . 2 2 − 4 × 0 . 1 7 × 8 5 = 1 5 . 0 8 1 0 0 5 0 0 . . . .
Next we calculate x 1 , the centre of disk 1 at the moment of collision, by using this value for t, to find x 1 = ( − 2 . 6 4 5 0 6 , 0 . 3 3 8 7 3 ) . Note that ∣ x 1 ∣ = 3 8 .
In order to find the solution for p 1 after the collision, we recall that ∣ p 1 ∣ must remain the same, while adding a momentum in the direction of x 1 . We can find this new p a f t e r by subtracting twice the projection of p 1 onto x 1 :
p a f t e r = p 1 − 2 ∣ x 1 ∣ 2 ( p 1 ⋅ x 1 ) x 1 .
This way we find p a f t e r = ( − 2 4 . 1 2 6 1 6 , 1 3 . 1 7 1 3 2 ) Check: ∣ p a f t e r ∣ = 2 7 . 4 8 7 3 7 is indeed unchanged.
So now the velocity of the green disk after the collision is 2 0 0 − p a f t e r = ( 0 . 1 2 0 6 3 , − 0 . 0 6 5 8 6 ) , still relative to the centre of mass, and adding the velocity of the centre of mass to this, we find the velocity relative to the axes: v y = 0 . 2 6 7 4 7 7
With this velocity, the time for the centre of the green disk to reach y=14 is 0 . 2 6 7 4 7 7 1 4 − − 2 . 4 7 5 7 = 6 1 . 5 9 6 7 6 seconds after collision. Adding this up to the time to collision, we find the answer of T=76.67776 s, so that the final answer is 7 6 6 7 7 .
I posted a 2D conservation problem recently, and since the particles had no size, the mathematics was under-constrained, and I had to add in additional constraints. This problem rectifies that by giving the objects size. Since the objects have size (and are circular), the impulses have to be equal and opposite, and they must be directed along the line connecting the two centers. Below is an outline of the solution steps:
1) "Run the simulation" to see where the disk centers are when they collide. The collision time and coordinates are given below (in the same units given in the problem):
t c ≈ 1 5 . 0 8 1 x 1 c ≈ − 2 . 4 5 9 4 9 y 1 c ≈ − 1 . 9 6 7 5 9 x 2 c ≈ 1 . 5 0 8 1 0 y 2 c ≈ − 2 . 4 7 5 6 9
2) At the time of collision, find the vector from one disk center to the other.
v x = x 1 c − x 2 c v y = y 1 c − y 2 c u x = ∣ v ∣ v x u y = ∣ v ∣ v y
3) Establish impulse direction vectors for the two disks
u 1 x = u x u 1 y = u y u 2 x = − u x u 2 y = − u y
3) The disks experience equal impulse magnitudes, and correspondingly, the velocity change for the second disk is half as big, since it has twice the mass. Use the "p" subscript to denote the post-collision values. Note that the "c"-subscripted values are given in the problem statement.
x ˙ 1 p = x ˙ 1 c + α u 1 x y ˙ 1 p = y ˙ 1 c + α u 1 y x ˙ 2 p = x ˙ 2 c + 2 1 α u 2 x y ˙ 2 p = y ˙ 2 c + 2 1 α u 2 y
4) Find α such that the energy and momentum conservation conditions are satisfied.
2 1 m 1 ( x ˙ 1 c 2 + y ˙ 1 c 2 ) + 2 1 m 2 ( x ˙ 2 c 2 + y ˙ 2 c 2 ) = 2 1 m 1 ( x ˙ 1 p 2 + y ˙ 1 p 2 ) + 2 1 m 2 ( x ˙ 2 p 2 + y ˙ 2 p 2 ) m 1 x ˙ 1 c + m 2 x ˙ 2 c = m 1 x ˙ 1 p + m 2 x ˙ 2 p m 1 y ˙ 1 c + m 2 y ˙ 2 c = m 1 y ˙ 1 p + m 2 y ˙ 2 p
5) Results:
α ≈ 0 . 5 1 2 0 7 5 x ˙ 1 p ≈ − 0 . 0 0 7 9 2 7 y ˙ 1 p ≈ 0 . 4 6 5 0 4 6 x ˙ 2 p ≈ 0 . 3 5 3 9 6 3 y ˙ 2 p ≈ 0 . 2 6 7 4 7 6
6) Update the velocity for the green disk (#2) and continue "running the simulation" until y 2 > 1 4 for the first time. This occurs at t ≈ 7 6 . 6 7 7