Two Inscribed Circles in a Right Triangle
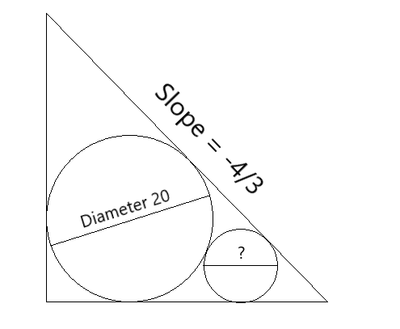
A right triangle has its legs parallel to the and axes as shown in the above figure. If the hypotenuse has a slope of , and the diameter of the bigger circle is , what is the diameter of the smaller circle? If the answer can be expressed as for positive integers with square-free, then find .
Diagram not drawn to scale
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the triangle be A B C with ∠ A = θ and the centers of the big and small circles be O and P respectively. Note that △ A B C is a 3 - 4 - 5 right triangle. Then we have:
A B = 1 0 cot 2 θ + 1 0 = 1 0 ⋅ 3 + 1 0 = 4 0 Note that tan 2 θ = sin θ 1 − cos θ = 5 3 1 − 5 4 = 3 1
Then B C = 4 3 × 4 0 = 3 0 . Let the radius of the small circle be r . And we have:
1 0 + ( 1 0 + r ) 2 − ( 1 0 − r ) 2 + r cot ( 2 9 0 ∘ − θ ) 1 0 + 4 0 r + r ( 1 − 3 1 1 + 3 1 ) 2 1 0 r + 2 r ( r ) 2 + 1 0 ⋅ r ( r + 2 1 0 ) 2 r ⟹ r = B C = 3 0 = 2 0 = 1 0 = 1 0 + 4 1 0 = 2 2 5 = 2 5 − 2 1 0 = 2 5 2 − 1 0 = 4 6 0 − 1 0 2 0 = 5 ( 3 − 5 )
Therefore the diameter of the small circle is 2 r = 1 0 ( 3 − 5 ) ⟹ a + b + c = 1 0 + 3 + 5 = 1 8 .