Two Kings Near the Edge: Open Problem #1
On a chessboard of a finite size, we want to place kings and knights such that each king attacks exactly 2 kings and 2 knights, and each knight attacks exactly 2 kings and 2 knights.
Is the following formation ever allowed on a finite board?
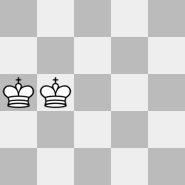
Note: the board may get expanded any finite amount up, down, and to the right.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
In my images, I’m going to use black pawns to mark squares that have to be empty, and white pawns to mark squares that need to have either a king or a knight, but it’s not yet clear which of the two.
The king that touches the edge still has to attack 2 more knights and 1 more king. There are two ways to place the knights:
1: place at least one knight in column A
The king on a3 already attacks 1 king and 1 knight, so 1 more king, and 1 more knight need to be placed on the squares b4, a2, and b2. The king on b3 already attacks 1 knight, 1 king, and it attacks the squares b4, a2, and b2, which will get the remaining 1 king and 1 knight it needs to attack. So the squares c4, c3, and c2 have to be empty.
However, the knight on a4 has to attack 4 pieces, and can attack only 4 squares, including the square c3. So the square c3 needs to be empty and have a piece at the same time. That’s a contradiction, which means it’s not allowed to place a knight in column A.
2: place both knights in column B and place the king in column A
The king on b6 already attacks 2 kings and 2 knights, so the squares c7, c6, and c5 have to be empty.
The king on a5 needs to attack 1 more knight. I can’t go on a4, because the knight would then only be able to attack 3 non-empty squares. So the knight has to go on b4, and a4 has to be empty.
The knight on b5 now attacks only 4 non-empty squares, so a3, c3, d4, and d6 all need to have some piece.
Let’s look at square c4. If it has a knight, it would attack 2 kings and the unknown pieces on a3 and d6, so those two need to be knights. But if that’s the case the knight on d6 would attack 3 knights: b7, b5, and c3. Therefore c4 isn’t allowed to have a knight.
Then how about a king? That king would then attack 2 knights, and the unknown pieces on c3 and d4. D3 and d5 would then have to be empty. However, the knight on b4 would then only be able to attack 3 non-empty squares. Therefore c4 has to be empty.
If the unknown piece on a3 would be a knight, it would attack 3 non-empty squares, so it has to be a king.
That king on a3 attacks only 4 non-empty squares, so a2, b2, and b3 need to have 2 kings and 1 knight on them. The piece on b3 isn’t allowed to be one of the kings, because it would then attack 5 pieces. Therefore the knight has to go on b3, and a2 and b2 are kings.
We’ve now reached a contradiction. The king on b2 attacks 4 pieces, so a1 and b1 have to be empty. However, the king on a2 is only attacking 3 pieces, so either a1 or b1 needs to have a knight. Therefore it’s also not allowed to place both knights in column B.
With that it has been proven that it’s not allowed to have two kings next to each other on the edge of a board.