Two Circles Kissing
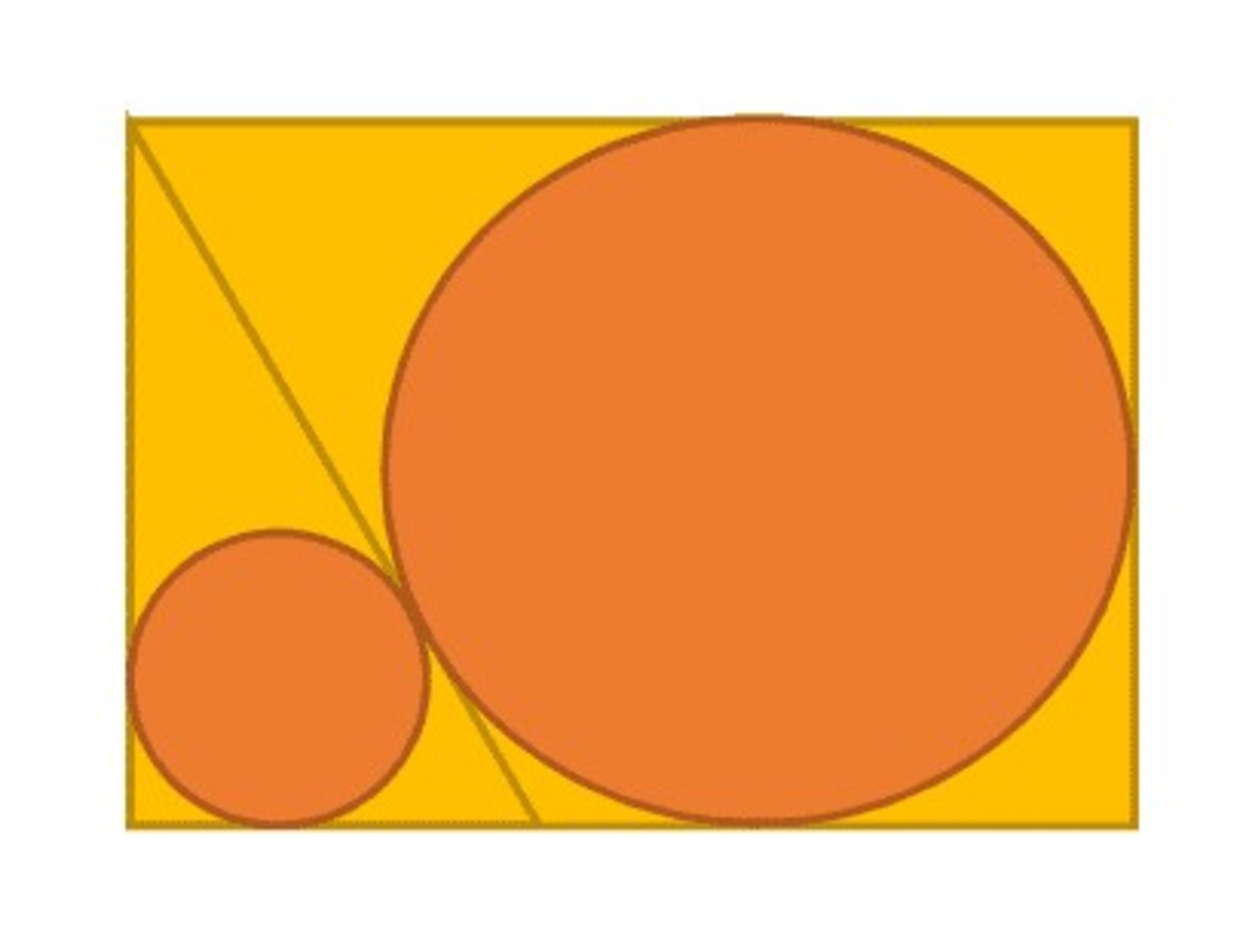
If the radius of the smaller circle is 1, find the radius of the larger circle.
Assume that both circles are tangent to the rectangle and are tangent to each other at a point where a straight line tangent to both of them goes through one of the vertices of the rectangle.
If the answer is in a format c a + b , where a , b , and c are positive integers and b does not contain a square, report a + b + c .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Choose the sides of the rectangle to be a & b (a<b) and let the radius of the larger circle be x. We can write down the following equations immediately: (a-1-x)²+(b-1-x)²=(1+x)², b=1+y+2√(x) since the common tangent between two circles of radii 1 & x is 2√(x). Moreover, the other common tanget passes through a vertex of the rectangle and thus, a-1=b-x. These three equations can be solved to obtain: a=3+√5, b=a²/4 and x = (3+√5)/2
I choose the point of osculation of the circles as the origin of a coordinate system. Note now that the small circle in the triangle is transformed into the large circle into a larger triangle by point reflection with factor r : ( x , y ) ↦ ( − r x , − r y ) .
The center of the small circle has coordinates ( − c , − s ) , with s , c > 0 and s 2 + c 2 = 1 .
The top-left corner of the triangle has coordinates ( − c − 1 , h ) . The line from the origin through this corner is tangent to the circles and therefore perpendicular to the radius. This gives the dot-product equation ( − c − 1 , h ) ⋅ ( − c , − s ) = 0 , with solution h = ( c + c 2 ) / s .
Upon transformation, the bottom of the small circle ( y = − s − 1 ) is transformed to the top of the large circle ( y = h ). This tells us that r ( s + 1 ) = s c + c 2 . Likewise, the top of the small circle ( y = 1 − s ) is transformed to the bottom of the large circle ( y = − 1 − s ). Thus r ( s − 1 ) = − 1 − s . Adding and subtracting these two equations, and multiplying them by s , we find { 2 r s 2 = c + c 2 − s 2 − s = ( c + s + 1 ) ( c − s ) 2 r s = c + c 2 + s 2 + s = c + s + 1 Divide the two: s = 2 r s 2 r s 2 = c + s + 1 ( c + s + 1 ) ( c − s ) = c − s . This gives c = 2 s so that c = 2 / 5 , s = 1 / 5 . Finally, r = 1 − s 1 + s = 5 − 1 5 + 1 = 4 6 + 2 5 = 2 3 + 5 . The answer, then, is a + b + c = 3 + 5 + 2 = 1 0 .
A D = K I = 2 r
A F = A D − F D = 2 r − 1
A K = A E = A F = 2 r − 1
D C = A B = A K + K B = ( 2 r − 1 ) + r = 3 r − 1
G I = D C − D G − I C = ( 3 r − 1 ) − 1 − r = 2 r − 2
G H = E H = I H = 2 1 × G I = 2 1 ( 2 r − 2 ) = r − 1
D H = D G + G H = 1 + ( r − 1 ) = r
A H = A E + E H = ( 2 r − 1 ) + ( r − 1 ) = 3 r − 2
A H 2 = A D 2 + D H 2
( 3 r − 2 ) 2 = ( 2 r ) 2 + r 2
3 r + 2 = 5 r
r = 3 − 5 2 = 2 3 + 5
3 + 5 + 2 = 1 0