Two layers down
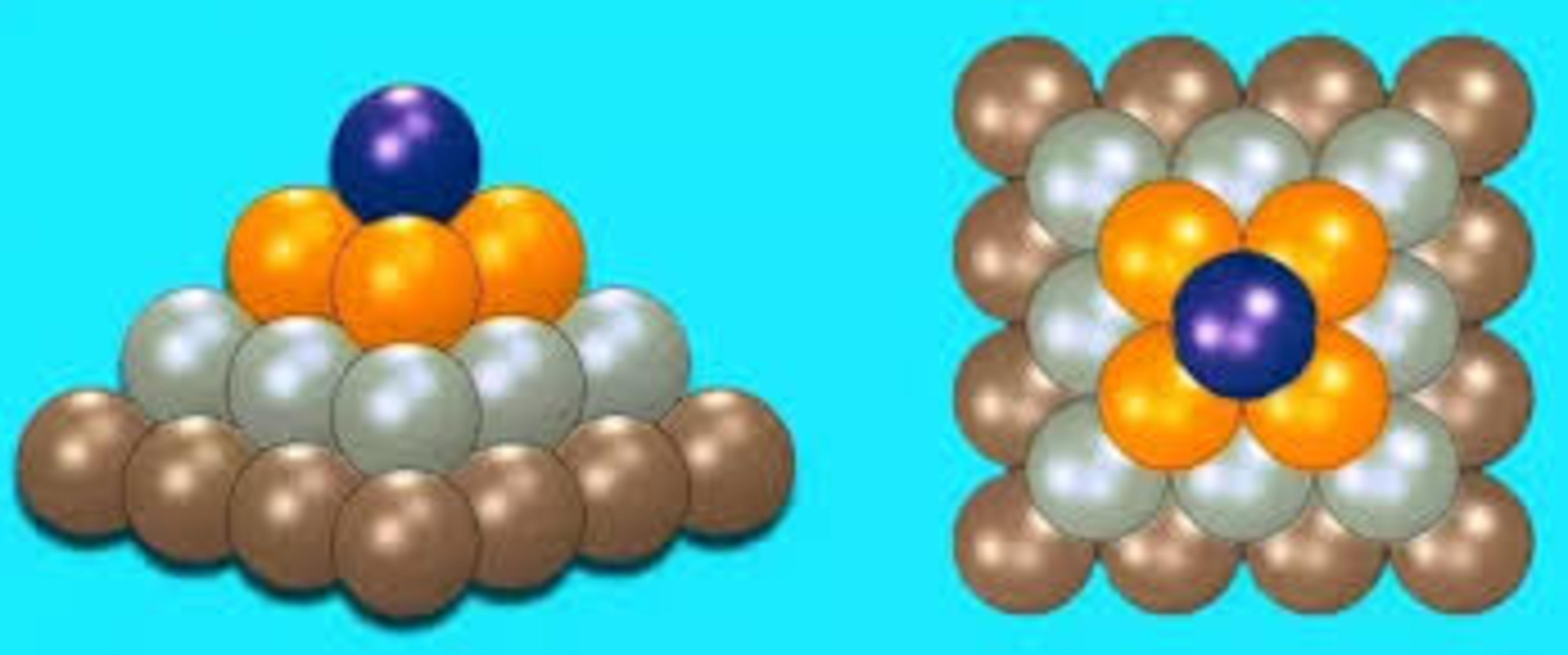
What is the (shortest) distance between the dark blue marble on top and the light blue marble directly below it (the one at the center of the 3 x 3 arrangement)?
Details: All the marbles are perfect unit spheres. The base of the arrangement is a regular rectangular grid in which all the neighboring spheres are tangent. Every sphere in layers 2 and up is supported by four other spheres.
Image credit: Wikipedia
The answer is 0.8284.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Lets start with the oranges spheres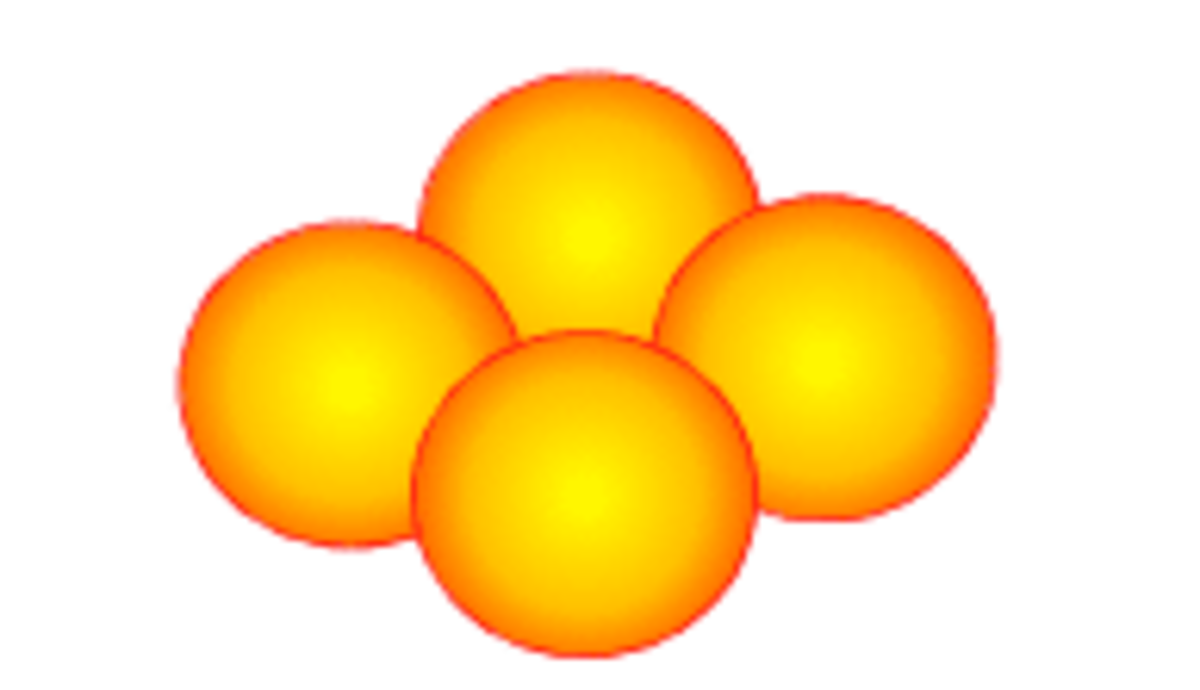
From above they look like this
Now add the dark blue above and light blue below
Looking at it edge on it will look like this
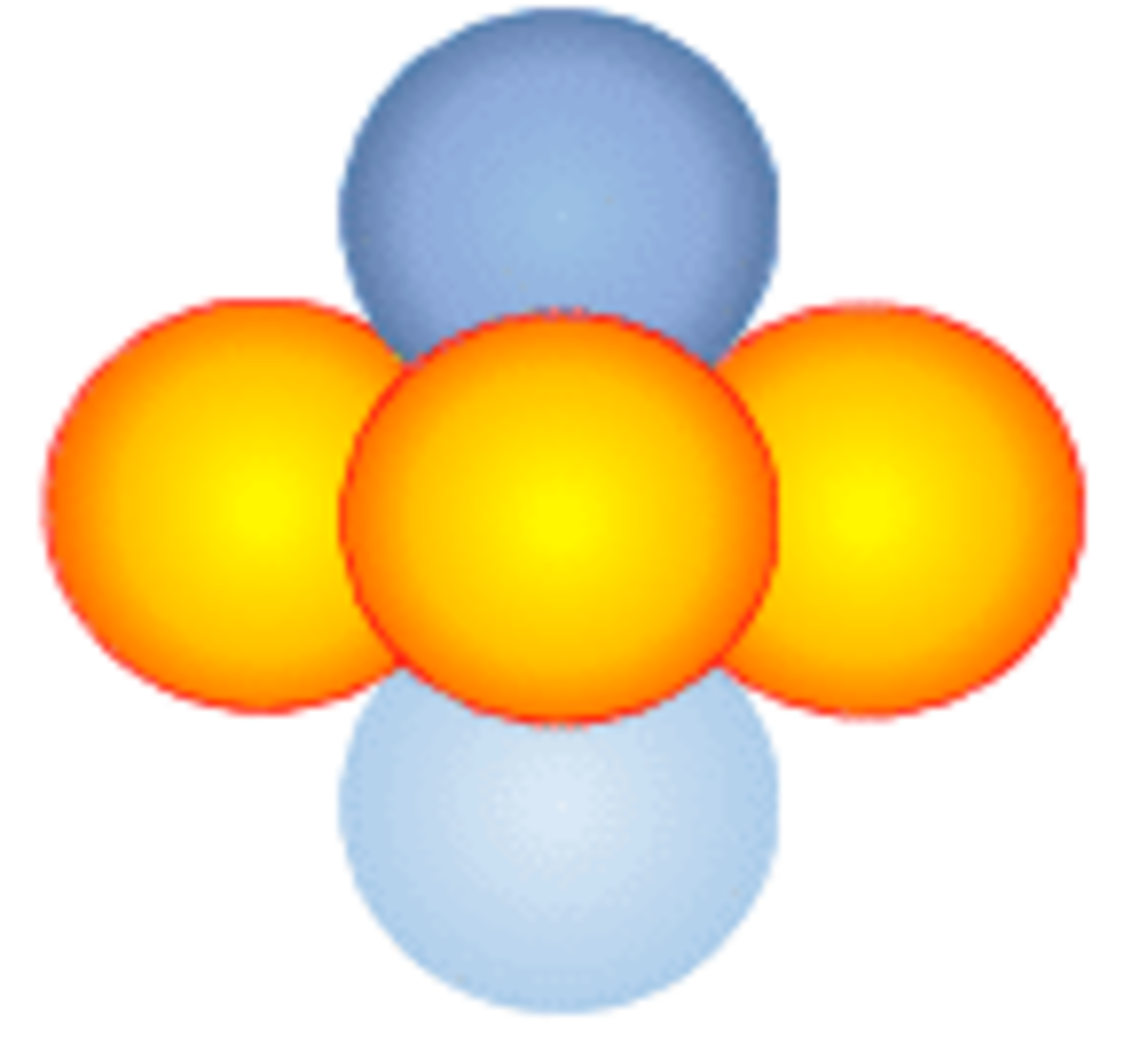And with the front orange sphere removed like this.
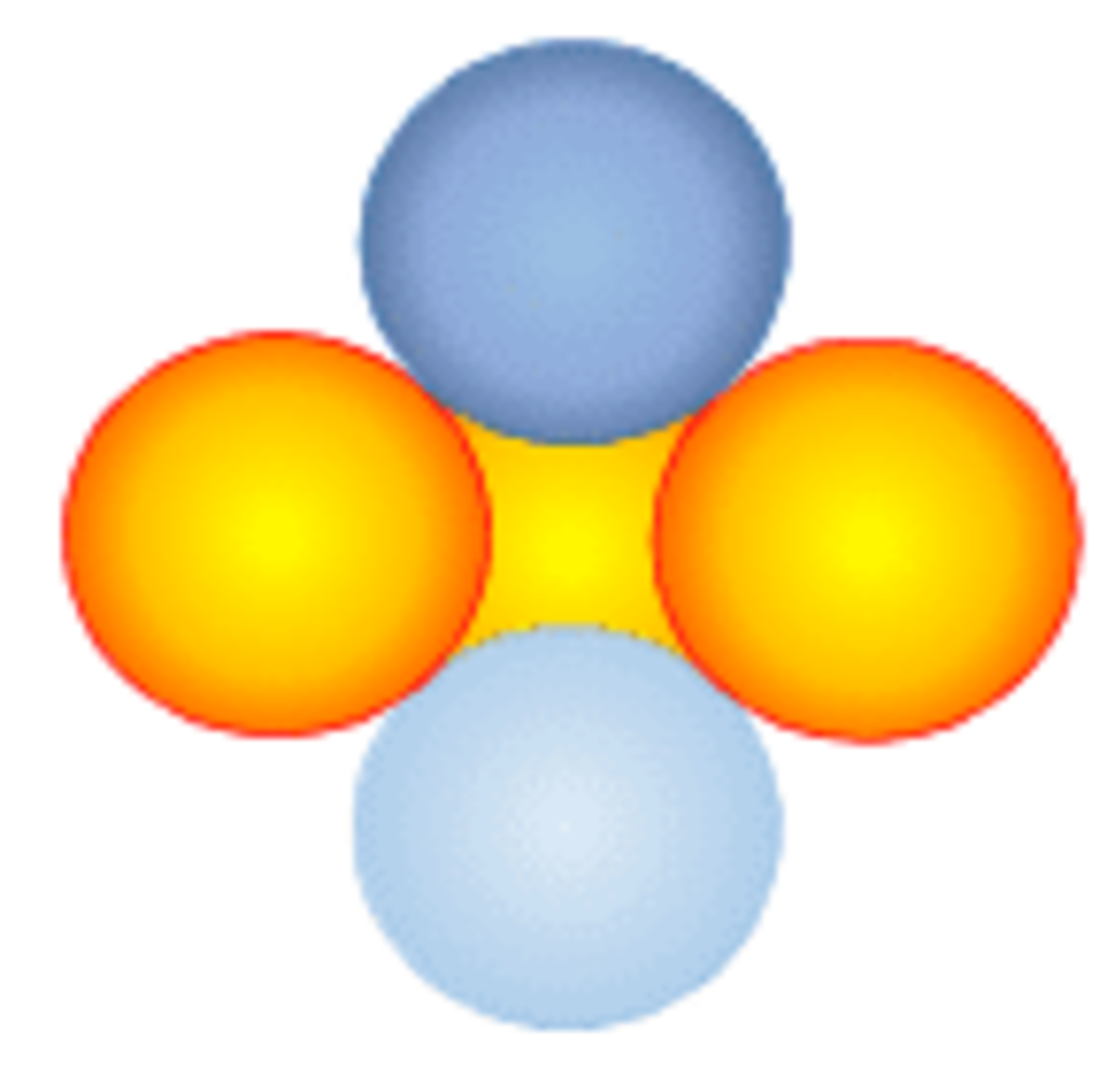We can see that the arrangement is just as symmetrical in the vertical plane as in the horizontal. The distance between the left and right orange spheres, determined by the square in the horizontal plane works to ensure a square in the vertical plane as well.
So the distance between the two blue marbles is the distance between their centers minus the two radii. Distance between the centers is the length of a diagonal in a square with a side 2, or 2 × 2 . The two radii add up to 2. So the distance is 2 × 2 − 2 = 0 . 8 2 8 4 .