Two Little Red Bombs
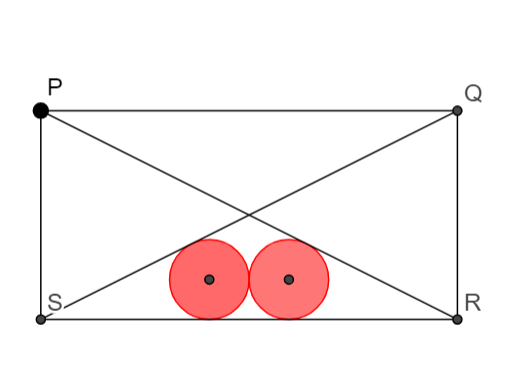
As shown above, the diagonals and are separately tangent to each of the red circles and the side is the common tangent to the two red circles. The two red circles are identical and their radii equal to units. Find the minimum area of the rectangle .
Try a non-calculus approach.
This is part of the set Things Get Harder! .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

To simplify our calculation, we might as why assume that the radius of circle is 1 unit and multiply the final answer by scale factor of ( 2 − 1 ) 2 .
By Pythagorean Theorem ,
( a + b ) 2 = ( 1 + a ) 2 + ( 1 + b ) 2
⇒ a 2 + 2 a b + b 2 = 1 + 2 a + a 2 + 1 + 2 b + b 2
⇒ 2 a b = 1 + 2 a + 1 + 2 b
⇒ a b = 1 + a + b
Let the area of rectangle P Q R S be A
A = 2 ( 1 + a ) ⋅ 2 ( 1 + b )
A = 4 ( 1 + a ) ( 1 + b )
A = 4 ( 1 + a + b + a b )
⇒ A = 4 ( a b + a b )
A = 8 a b
By AM-GM Inequality ,
2 a + b ≥ a b
a + b ≥ 2 a b
a + b + 1 ≥ 2 a b + 1
a b ≥ 2 a b + 1
( a b ) 2 − 2 a b − 1 ≥ 0
When ( a b ) 2 − 2 a b − 1 = 0 ,
a b = 2 2 ± 4 + 4 = 2 2 ± 8 = 2 2 ± 2 2 = 1 ± 2
∴ ( a b − ( 1 + 2 ) ) ( a b − ( 1 − 2 ) ) ≥ 0
⇒ a b ≤ 1 − 2 (impossible)
or
a b ≥ 1 + 2
⇒ a b ≥ ( 1 + 2 ) 2
∴ A = 8 a b ≥ 8 ( 2 + 1 ) 2
Returning to our original question, the minimum area of rectangle P Q R S (reinstated) = 8 ( 2 − 1 ) 2 ( 2 + 1 ) 2 = 8 ( 2 − 1 ) 2 = 8
Clarification: The equality holds if and only if a = b , which asserts the fact that rectangle P Q R S is a square if and only if its area is minimum.