Two Magnetic Fields

Electricity and Magnetism Level pending

In the $xy$ -plane , the region $y>0$ has a uniform magnetic field $B_1 \vec{k}$ and the region $y<0$ has another uniform magnetic field $B_2 \vec{k}$ . A positively charged particle is projected from the origin along the positive $y$ -axis with speed $v_0=πms^{-1}$ at $t=0$ as shown in the figure .

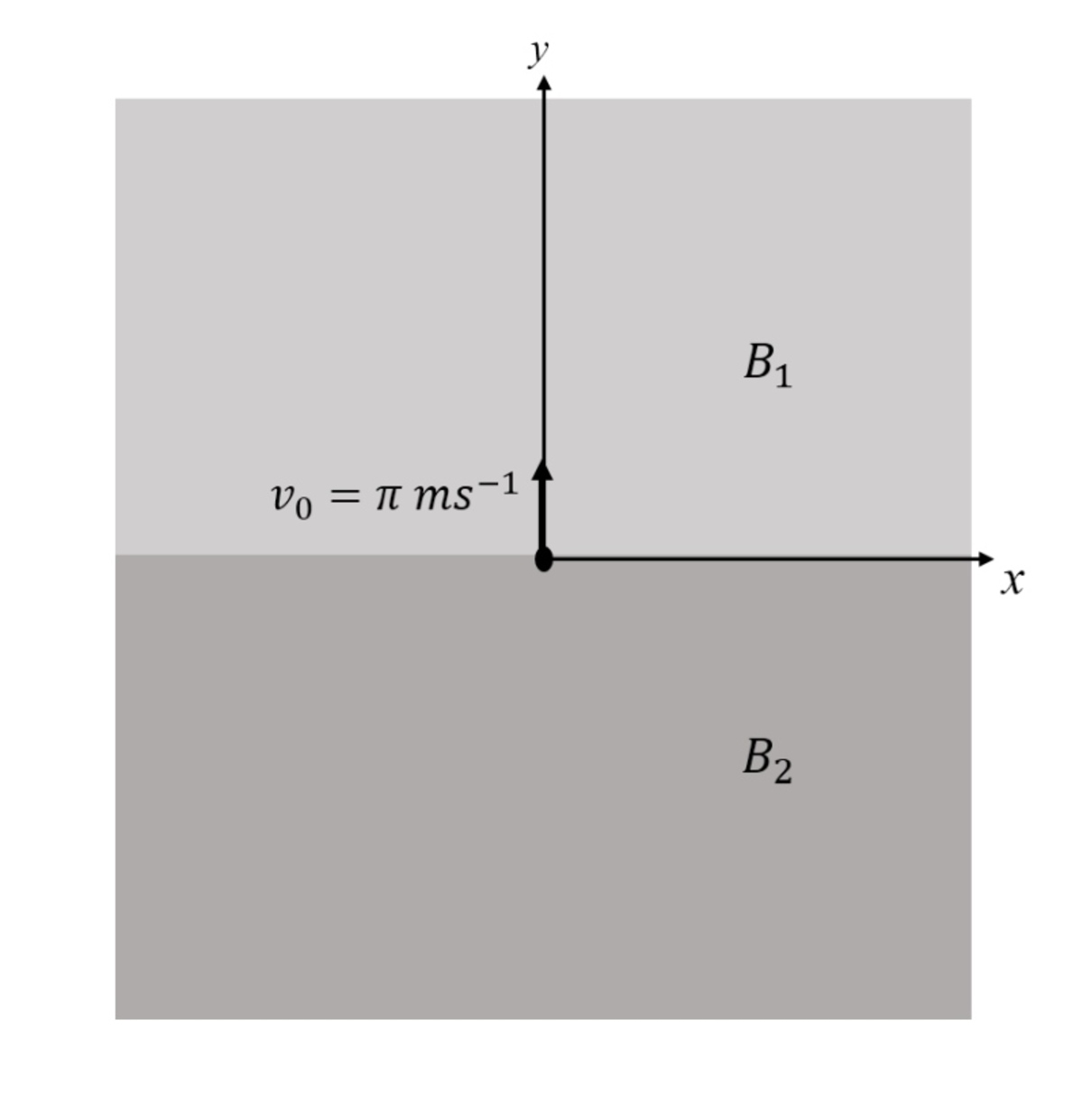
Let $t=T$ be the time when the particle crosses the $x$ axis from below for the first time. If $B_2=4B_1$ , the average speed of the particle, in $ms^{-1}$ , along the $x$ -axis in the time interval $T$ is ?

Details and Assumptions
1) Neglect gravity

The problem is not original.

The answer is 2.

1 solution

A Former Brilliant Member
May 28, 2020

In the region with magnetic flux density $\vec B_1$ , the differential equations of motion of the particle are

$\dfrac{dv_x}{dt}=\dfrac{qB_1}{m}v_y, \dfrac{dv_y}{dt}=-\dfrac{qB_1}{m}v_x$ .

Solving these using initial conditions we get $v_x=v_0\sin (\frac{qB_1t}{m})$ .

In the region where the magnetic flux density is $B_2$ , the $x$ -component of velocity is similarly

$v_0\sin (\frac{qB_2t}{m})$ .

The time period in the first case is $\dfrac{2πm}{qB_1}$ and in the second case is $\dfrac{2πm}{qB_2}$ .

Hence the average speed of the particle in the $x$ direction is

$\dfrac{qv_0}{πm(\frac{1}{B_1}+\frac{1}{B_2})}\times \dfrac{2m}{q}(\frac{1}{B_1}+\frac{1}{B_2})=\dfrac {2v_0}{π}=\boxed 2$ ms $^{-1}$ .

Two Magnetic Fields

The answer is 2.

1 solution

1 pending report

Vote up reports you agree with