Two Mating Parabolas
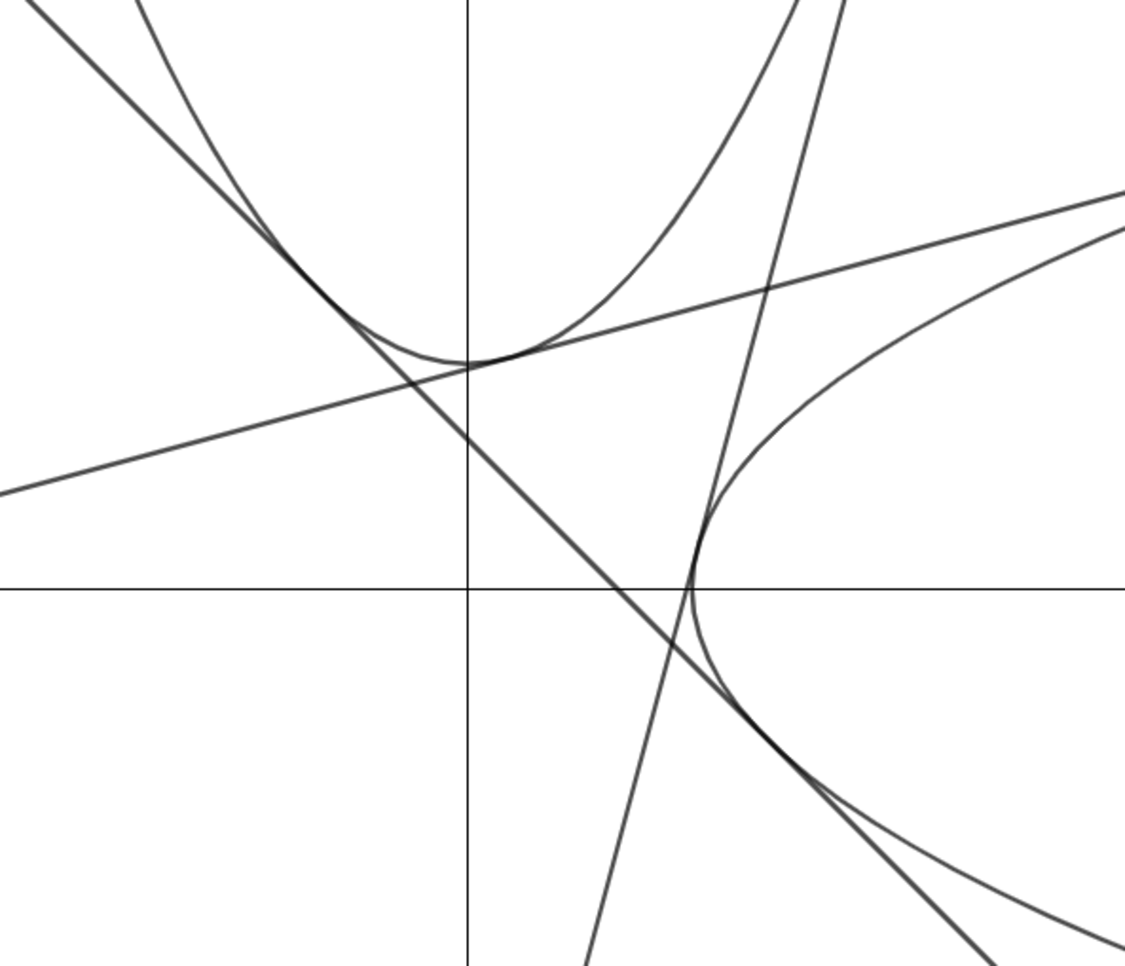
The parabolas of the form y = x 2 + a and x = y 2 + a , where a is a real-valued constant, are positioned such that three lines tangent to both parabolas form an equilateral triangle.
If the area of the triangle is unique and can be expressed as B A C , where A , B , and C are positive integers, g cd ( A , B ) = 1 and C is square free, input the product A B C as your answer.
The answer is 72.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
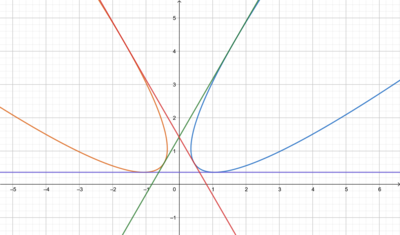
Note that the graph is symmetric in the line y = x . One nice approach here is to rotate everything by 4 5 ∘ . We can do this with the variable change x = 2 u + v , y = 2 v − u
(the 2 s in the substitution ensure there's no scaling). Our equations become 2 v − u = 2 ( u + v ) 2 + a and 2 u + v = 2 ( v − u ) 2 + a
These look worse, but the graph (in u v coordinates) is now
There is a shared horizontal tangent. To form an equilateral triangle, all we need to do is make sure one of the other shared tangents has gradient tan 6 0 ∘ = 3 .
There are several ways to go from here; implicit differentiation works well but we can try without calculus.
For a line v = m u + c to be tangent to a parabola, it has to meet it in exactly one point. This means the equation we get by substituting for v has to have exactly one root. Since with a parabola we expect a quadratic equation, this is the same as saying the discriminant of that quadratic has to be zero.
In this case, substituting v = m u + c into the equations for the first parabola, we get 2 m u + c − u = 2 ( u + m u + c ) 2 + a
(which is indeed a quadratic in u ). Setting the discriminant to zero gives 1 − 4 a + 4 2 c − 2 m − 8 a m + 4 2 c m + m 2 − 4 a m 2 = 0
Now, when m = 0 , this is just 1 − 4 a + 4 2 c = 0
so the horizontal tangent has equation v = 4 2 4 a − 1
Substituting m = 3 , we get 4 − 2 3 − 1 6 a − 8 3 a + 4 2 c + 4 6 c = 0
Doing the same for the second parabola, we get 4 + 2 3 − 1 6 a + 8 3 a + 4 2 c − 4 6 c = 0
These are just linear simultaneous equations in a and c ; solving, we find a = 4 3 and c = 2 .
Finally, the three tangents have equations v = 2 2 1 , v = 2 ± u 3
The easiest way to work out the area of the equilateral triangle is just to note its height is 2 − 2 2 1 , from which the area is 8 3 3 and the answer to the problem is 7 2 .
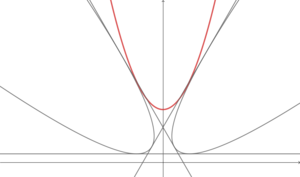
Bonus question: the equation of the red parabola is v = u 2 + k ; what's k ?
Log in to reply
Given the values you found from the solution, k = 4 3 + 2 .
By symmetry, the graph is reflective in y = x , and the slopes of the three lines will be tan − 1 1 3 5 ° = − 1 , tan − 1 1 5 ° = 2 − 3 , and tan − 1 7 5 ° = 2 + 3 .
Let the line with a slope of 2 + 3 have an equation of y = ( 2 + 3 ) x + b . Since it is tangent to both parabolas, the discriminants of both ( 2 + 3 ) x + b = x 2 + a and x = ( ( 2 + 3 ) x + b ) 2 + a will be zero, so − 4 a + 4 b + 4 3 + 7 = 0 and − 4 ( 7 + 4 3 ) a − 4 ( 2 + 3 ) b + 1 = 0 .
These two equations solve to a = 4 3 and b = − 1 − 3 , so the equations of the parabolas are y = x 2 + 4 3 and x = y 2 + 4 3 , and the equation of this line is y = ( 2 + 3 ) x − 1 − 3 .
The equilateral triangle has a vertex on the lines y = ( 2 + 3 ) x − 1 − 3 and y = x , which solves to ( 1 , 1 ) .
Now let the line with a slope of − 1 have an equation of y = − x + c . Since it is tangent to the parabola y = x 2 + 4 3 , the discriminant of − x + c = x 2 + 4 3 will be zero, so c − 2 1 = 0 , which solves to c = 2 1 , making the equation of this line y = − x + 2 1 .
The midpoint of the base of the equilateral triangle is on the lines y = − x + 2 1 and y = x , which solves to ( 4 1 , 4 1 ) .
By the distance formula, the height of the equilateral triangle between ( 4 1 , 4 1 ) and ( 1 , 1 ) is 4 3 2 , which makes one of its sides 3 2 ⋅ 4 3 2 = 2 6 , and its area 4 3 ( 2 6 ) 2 = 8 3 3 .
Therefore, A = 3 , B = 8 , C = 3 , and A B C = 7 2 .