Two paths on a halfsquare
On isosceles triangle A B C with right angle at C , the green and purple paths are the same length.
In other words, A P + P B = A C + C P .
If B C B P can be written as c a − b with a , b , c integers, a > 0 , and b square-free, then what is a + b + c ?
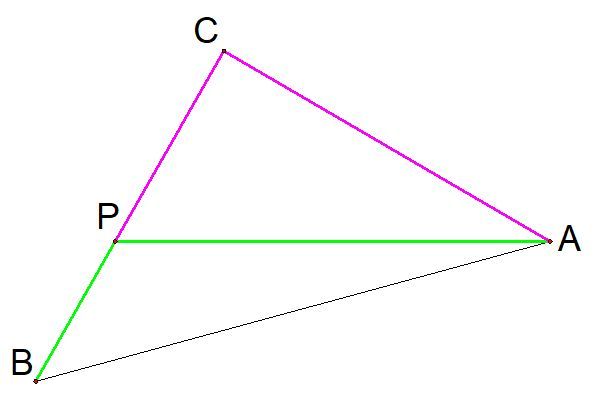
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Much more elegant than my solution. Thanks!
Let B be the origin, A=(2,0), C=(1,1), and P=(p,p). The ratio sought is equivalent to the x-coordinate of P.
The green path has length 2 p + ( p − 2 ) 2 + p 2
The purple path has length 2 ( 1 − p ) + 2
Set the two equal and divide both sides by 2
p 2 − 2 p + 2 = 2 − 2 p
Square both sides then use the quadratic formula to get
p = 3 3 − 3
From which we have a = 3 , b = 3 , c = 3 and a + b + c = 9
B C B P is given by x x − y = y 3 y 3 − y = 3 3 − 1 = 3 3 − 3
⇒ a = b = c = 3 , Hence a + b + c = 9