Two Perpendicular Chords
In circle Γ , two chords A B , C D are perpendicular at E . We have A E = 3 , E B = 7 , E C = 1 . Let the radius of Γ be R . What is the value of R 2 ?
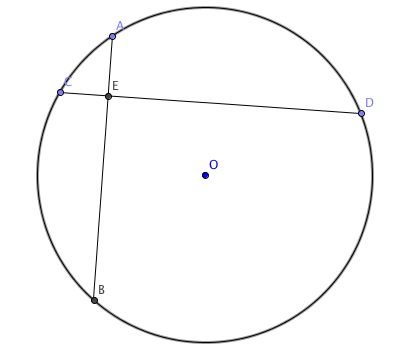
The answer is 125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
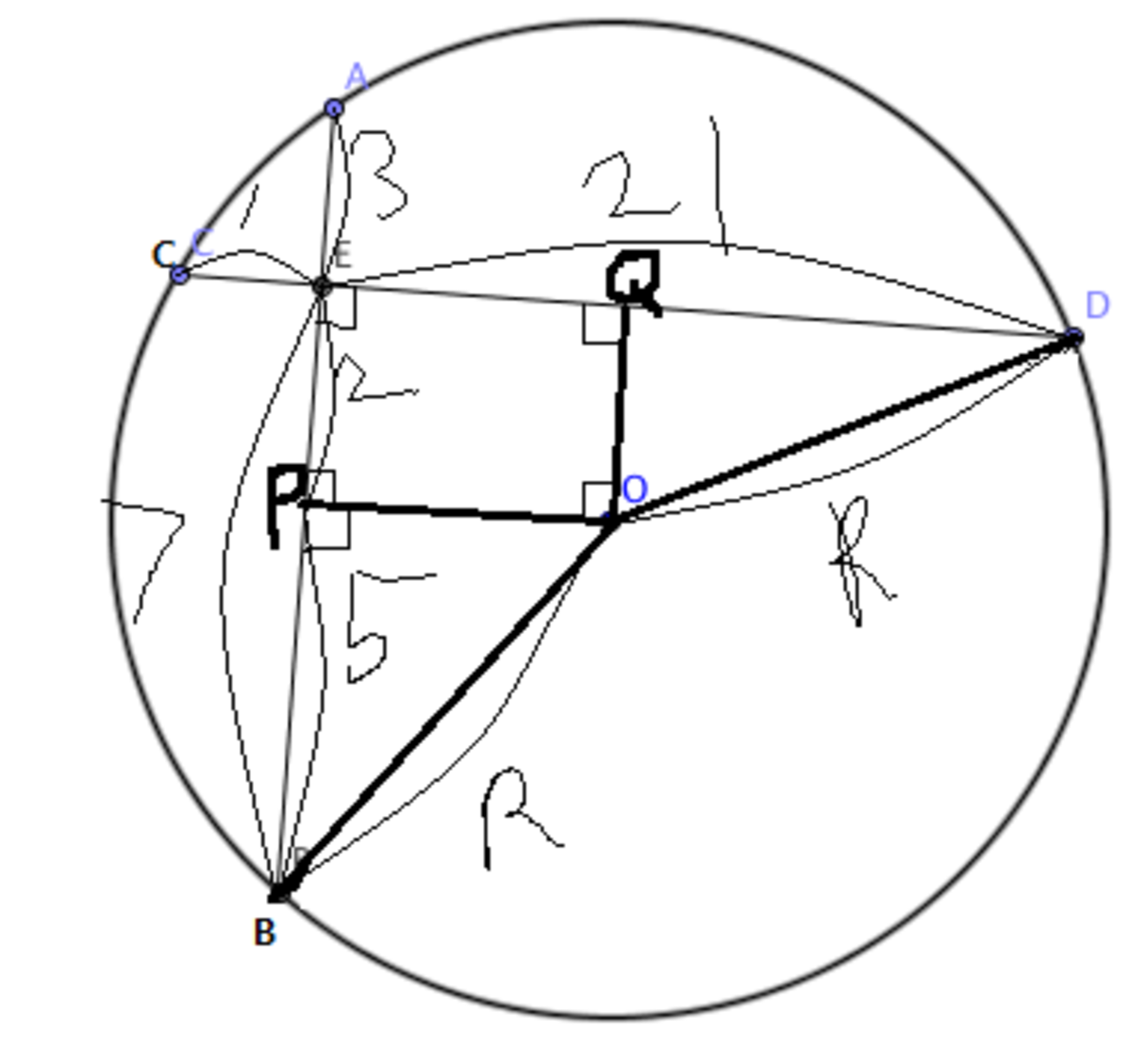
A diagram helps a lot in this problem. By the intersecting chord theorem we have A E × E B = E C × E D . On substituting values we have 7 × 3 = 1 × E D which gives us the value of E D as 2 1 . Therefore length of chord C D = 2 2 . Draw perpendicular lines from midpoint of these two chords. Obviously the point where the lines intersect is the centre of the circle. Let the centre be O . Let the midpoint of the chord A B and C D be M and N respectively. Since the chords are perpendicular, the quadrilateral E N O M is a rectangle. Hence O N = E M = A M − A E = 5 − 3 = 2 We know that this distance A M is 5 units because, perpendicular line from the centre of the circle to the chord bisects the chord. Since chord length A B = 1 0 , A M = 5 , therefore O N = 2 Similarly, O N bisects chord C D and hence length N D = 1 1 . Join the points O D which is the radius. This gives us a right angled triangle with lengths of the legs as 2 and 1 1 . Therefore by pythagoras theorem, radius O D = 1 1 2 + 2 2 = 1 2 1 + 4 = 1 2 5
The hard part of this question was to figure out how to related the radius of the circle to these seemingly random points. Those who know the extended sine rule can proceed directly. Otherwise, you can find the center of the circle by looking at the intersection of perpendicular bisectors of two chords.
let A,B,C,D,E be points on a cartesian plane, such that the conditions given in the problem hold, and AB lie on the x-axis, CD lie on the y-axis, and C is the origin (0,0). Without loss of generality, we can let A = (-3,0), B = (7,0), C = (1,0). By the power of point E over circle Gamma, we have AE EB = CE ED, hence ED = 21, so D = (0,-21).
Let O be the center point of the circle. the line passing through O and perpendicular to AB (parallel to y-axis) must bisect AB (because Gamma is a circle), hence the x-coordinate of O must be equal to that of the midpoint of AB, which is 2. By similar argument, the line passing through O and perpendicular to CD must bisect CD, and hence the x-coordinate of O must be -10.
R = distance between O (2,-10) and A (-3,0) = sqrt(125), hence R^2 = 125.
We see that our circle circumscribes triangle ABC, which has a base length of 10 and a height of one. Thus, the area of triangle ABC is 5. We can also solve for BC and AC using the Pythagorean Theorem, which are 5sqrt2 and sqrt10 respectively. Given that the area of a triangle is equal to the product of its sides divided by 4 times the circumradius, we have 5 = 100sqrt5/4R. Isolating R, we have R = 5sqrt5, so R^2 = 125.
Start by using the power of point theorem on AE, EB, EC, to find that ED must be equal to 21, thus the entire length of AD must be equal to 22. Let the midpoint of AB be P. Draw the diameter of the circle from point P. By Symmetry Half of chord AD must be equal to 11, let the midpoint of this chord be Q, taking out part of AE leaves 10. It is easy to see that point Q is co-linear with the enter of the circle. Using the Pythagorean theorem on point B with P and the center of the circle, we know one leg is 5 and that the length of P to Q is 10. Thus the answer after using the Pythagorean theorem with the radius being the hypotenuse is 125.
Consider a circle of centre O with four different points a,b,c,d join ad and bc. triangle ade and bce are similar as angle aec=angle bec=90 angle ade= angle cbe(angles in the same segment of the arc ac) using similarity of triangles de=21 draw of perpendicular to ab and og perpendicular to cd. triangle oaf is congruent to triangle obf since oa=ob(radius) angle ofa=angle obf(90) of common side so f is the midpoint of ab af=5
similarly cg=11 cg=ce+eg eg=of(parallel) this gives of of=10. in right angle triangle oaf applying pythagoras theorem gives radius squared as 100+25=125.
Label the midpoint of CD = P. OP is the perpendicular bisector of CD.
By the two-chord theorem, CG GD = AE EB = 21, so ED = 21. So, CD = 22, and PE = 10
Now draw OQ, where Q is the midpoint of AB.
QB = AB/2 = 5, and OQ = 11-1 = 10
10^2 + 5^2 = R^2 =125
Let the centre be O, and let the midpoints of the chords AB and CD be F and G respectively; and let EF = x.
Since OGEF form a rectangle, EG = OF and EF = OG, so we have OG = x, and EG = OF = 2.
Now consider the right-angled triangles OCG and OAF. We have R^2 = 25 + x^2 from OCG and R^2 = 4+ (x+1)^2 from OAF.
Solving for x gives x = 10, and thus we have R^2 = 125.
Let the midpoint of CD = F. Therefore, OF is the perpendicular bisector of CD.
By using two-chord theorem, CG GD = AE EB = 21 So, ED = 21. Then, CD = 22, and FE = 10
Next, draw OG, where G is the midpoint of AB.
GB = AB/2 = 5, and OG = 11-1 = 10
R^2= 10^2 + 5^2 R^2=125
Label the midpoint of CD = P. OP is the perpendicular bisector of CD.
By the two-chord theorem, CG GD = AE EB = 21, so ED = 21. So, CD = 22, and PE = 10
Now draw OQ, where Q is the midpoint of AB.
QB = AB/2 = 5, and OQ = 11-1 = 10
10^2 + 5^2 = R^2
(Please draw a diagram to understand the answer better)
Using intersecting chord theorem, we know A E × E B = C E × E D
From this we get E D = 2 1
Now from center O drop O M p e r p e n d i c u l a r t o A B and O N p e r p e n d i c u l a r t o C D
Therefore as Radius bisects chord , implies N C = 1 1 and as E C = 1 , i m p l i e s N E = N C − E C = 1 0
Therefore as O M E N is a rectangle so, O M = 1 0 and M B = 5 as radius bisects chord ( we, know AB = 7+3= 10)
Now O B = R , so by using Pythagoras theorem,
O
B
2
=
M
B
2
+
O
M
2
O
B
2
=
1
0
2
+
5
2
O B 2 = R 2 = 1 2 5
First, by the power-of-point theorem, \overline{AE} \times \overline{EB} = \overline{CE} \times \overline{ED} 3 \times 7 = 1 \times \overline{ED} \rightarrow \overline{ED} = 21 Since 3 points (or a triangle) define a unique circle, the circumradius of triangle CBD is the radius of circle \gamma The circumradius of any triangle is given by the formula A = \frac{abc}{4R} where R is the circumradius, A is the area and a, b, and c are the side lengths of the triangle. Because \overline{AB} is perpendicular to \overline{CD} the area of triangle CBD is \frac{7 \times 22}{2} = 77 We can find \overline{CB} and \overline{BD} by Pythagorean theorem which yields \overline{CB} = 5\sqrt{2} and \overline{BD} = 7\sqrt{10} We can now use our formula: 77 = \frac{5\sqrt2 \times 7 \sqrt10 \times 22}{4R} Solving for R yields 5\sqrt{5}. R^2 = 125
I first generalized the problem and came up with this. If two chords of a circle with length 2 a and 2 b units respectively intersect and right angles and the point of intersection being c units away from the centre of the circle, we have R , the radius of the circle
= 2 a 2 + b 2 + c 2 .
The following solution is more or less same as the proof of the above statement. First of all we use the secant property which says for two intersecting chords of a circle, namely A B and C D intersecting at E , we have A E × E B = C E × E D . WE use this to find the value of E D which is E C A E × E B = 2 1 . Now, we drop draw O X ⊥ C D and O Y ⊥ A B . Thus we have C X = X D = 2 2 2 = 1 1 = a (say). Therefore, we have E X = 1 0 . On the other hand, we have B Y = Y A + 5 = b (say) and we have E Y = 5 − 3 = 2 . We also notice that E X O Y is a rectangle and we assume E X = O Y = x and O X = E Y = y . Thus we have O D 2 = E X 2 + E Y 2 = x 2 + y 2 = 1 0 2 + 2 2 . We will need this later. We join O , D and O , B . In right angles triangles O Y B and O X D we have,
O Y 2 + Y B 2 = O B 2
⟹ x 2 + b 2 = R 2 ... (i) and we have
O X 2 + X D 2 = O D 2
⟹ y 2 + a 2 = R 2 ...(ii)
Adding (i) and (ii) we have,
2 R 2 = b 2 + a 2 + x 2 + y 2 = 5 2 + 1 1 2 + 1 0 2 + 2 2 = 2 5 0
Thus R 2 = 1 2 5 .
To find E D , we multiple the segments of each chord:
7 ( 3 ) = 1 ( E D ) , therefore E D = 2 1
To find the the radius, we use the formula:
4 R 2 = A E 2 + E B 3 + C E 2 + E D 2
Substitute the values of each segment then divide by 4.
 F
i
r
s
t
,
d
r
a
w
i
n
t
h
e
l
i
n
e
s
a
s
s
h
o
w
n
o
n
t
h
e
d
i
a
g
r
a
m
.
O
i
s
t
h
e
c
e
n
t
e
r
o
f
t
h
e
c
i
r
c
l
e
.
O
P
a
n
d
O
Q
a
r
e
p
e
r
p
e
n
d
i
c
u
l
a
r
t
o
A
B
a
n
d
C
D
,
r
e
s
p
e
c
t
i
v
e
l
y
.
B
y
"
I
n
t
e
r
s
e
c
t
i
n
g
C
h
o
r
d
T
h
e
o
r
e
m
"
,
A
E
×
E
B
=
C
E
×
E
D
→
3
×
7
=
1
×
E
D
→
E
D
=
2
1
B
y
"
C
h
o
r
d
B
i
s
e
c
t
i
o
n
T
h
e
o
r
e
m
"
,
A
P
=
P
B
∴
B
P
=
5
→
E
P
=
2
.
N
o
w
,
n
o
t
i
c
e
t
h
a
t
□
E
Q
O
P
i
s
a
r
e
c
t
a
n
g
l
e
.
S
o
,
w
e
c
a
n
s
a
y
t
h
a
t
O
P
=
E
Q
a
n
d
E
P
=
O
Q
∴
E
D
=
E
Q
+
Q
D
=
O
P
+
Q
D
=
O
B
2
−
B
P
2
+
O
D
2
−
O
Q
2
=
O
B
2
−
B
P
2
+
O
D
2
−
E
P
2
⟶
2
1
=
R
2
−
5
2
+
R
2
−
2
2
∴
R
2
=
1
2
5
F
i
r
s
t
,
d
r
a
w
i
n
t
h
e
l
i
n
e
s
a
s
s
h
o
w
n
o
n
t
h
e
d
i
a
g
r
a
m
.
O
i
s
t
h
e
c
e
n
t
e
r
o
f
t
h
e
c
i
r
c
l
e
.
O
P
a
n
d
O
Q
a
r
e
p
e
r
p
e
n
d
i
c
u
l
a
r
t
o
A
B
a
n
d
C
D
,
r
e
s
p
e
c
t
i
v
e
l
y
.
B
y
"
I
n
t
e
r
s
e
c
t
i
n
g
C
h
o
r
d
T
h
e
o
r
e
m
"
,
A
E
×
E
B
=
C
E
×
E
D
→
3
×
7
=
1
×
E
D
→
E
D
=
2
1
B
y
"
C
h
o
r
d
B
i
s
e
c
t
i
o
n
T
h
e
o
r
e
m
"
,
A
P
=
P
B
∴
B
P
=
5
→
E
P
=
2
.
N
o
w
,
n
o
t
i
c
e
t
h
a
t
□
E
Q
O
P
i
s
a
r
e
c
t
a
n
g
l
e
.
S
o
,
w
e
c
a
n
s
a
y
t
h
a
t
O
P
=
E
Q
a
n
d
E
P
=
O
Q
∴
E
D
=
E
Q
+
Q
D
=
O
P
+
Q
D
=
O
B
2
−
B
P
2
+
O
D
2
−
O
Q
2
=
O
B
2
−
B
P
2
+
O
D
2
−
E
P
2
⟶
2
1
=
R
2
−
5
2
+
R
2
−
2
2
∴
R
2
=
1
2
5
Since A B and C D are the chords of the circle Γ , the point A , B , C , and D are on the circle Γ 's perimeter.
A B and C D are perpendicular at E , so it can be seen that triangle A B C has base A B and vertical height C E .
Using Pythagoras' theorem,
B C is E B 2 + E C 2 = 7 2 + 1 2 = 5 0 = 5 2
and A C is E A 2 + E C 2 = 3 2 + 1 2 = 1 0 .
Since point A , B , and C are on the circle Γ 's perimeter, the circle Γ is the circumcircle of a triangle A B C .
If we know the length ( a , b , c ) of the three sides of the triangle, the radius of its circumcircle is :
R = 4 × A a b c
A = Area of Triangle.
So the radius of circle Γ is :
R = 4 × 2 1 × b × h A B × B C × C A
R = 4 × 2 1 × ( 3 + 7 ) × 1 ( 3 + 7 ) × 5 2 × 1 0
R = 2 0 1 0 0 5
R = 5 5
So, R 2 = 1 2 5 .