Two points And A Circle Of Life!
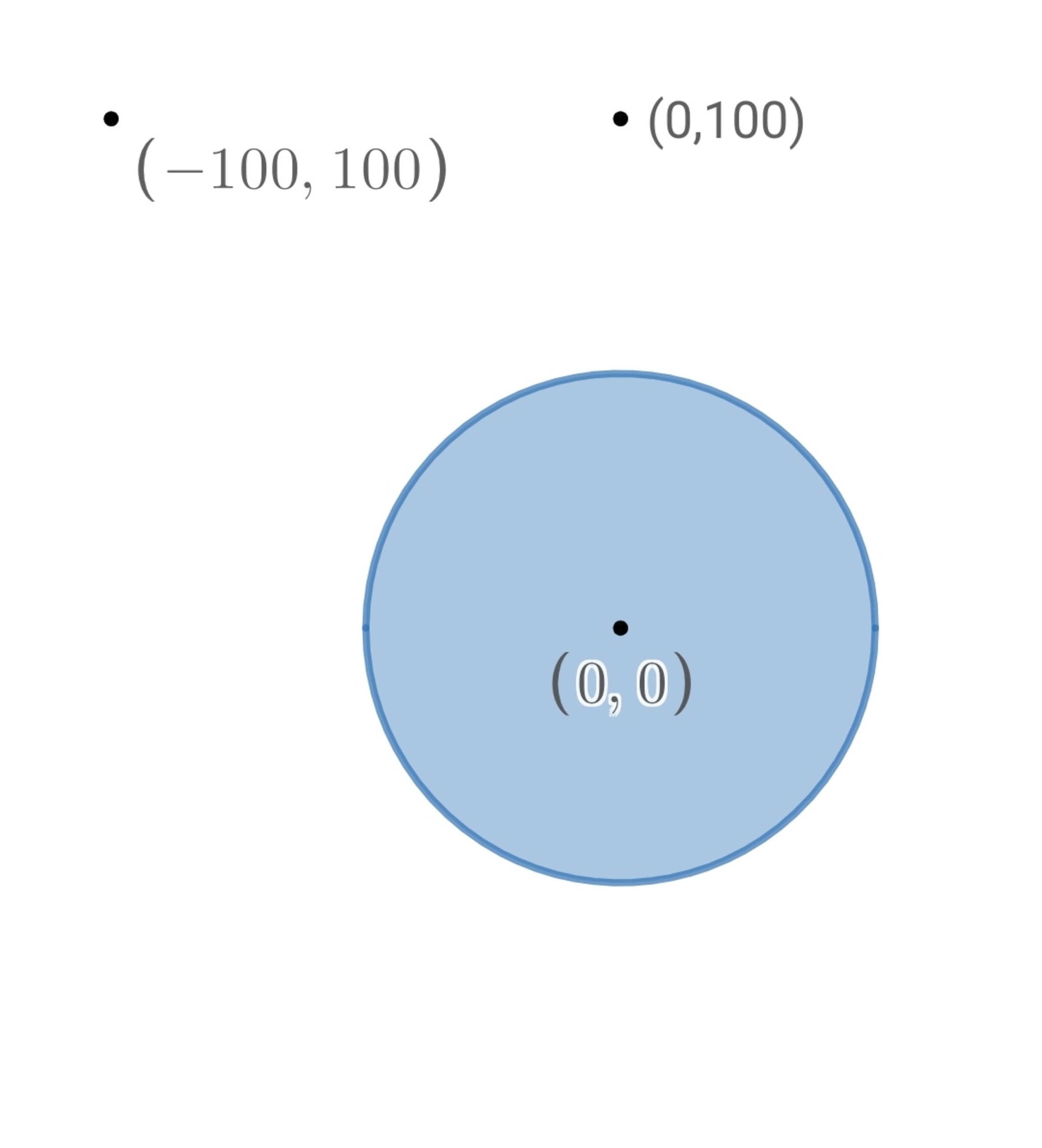
A person wants to go from point to edge of a circular pond of radius and center to fill water. From there, he goes to point . You can't swim and so you can't go inside circular pond and only go to it's edge to fill water.
If the length of the shortest path for above process is , Enter answer as where denotes Floor Function
Try similar problems
- Ellipse's Circular Tangents
- Ellipse's Circumscribed Perimeter
- Highly Elliptical Area
- Areal Parabolic Centroid
- Co-Normal Parabolic Centroid
All of my problems are original .
The answer is 154.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For shortest path, we have to go straight line to circle and then straight line to ( 0 , 1 0 0 )
We know that a curve who sum of distances from two points is constant is an ellipse
Let's build ellipses with P ( − 1 0 0 , 1 0 0 ) and Q ( 0 , 1 0 0 ) as foci till it touches the circle as at that point, sum of distances is minimum.
Now, if ellipse touches circle at point R , then ray P R after reflection from ellipse will pass from Q by reflexion property of ellipse. Now, as circle and ellipse touch each other, at contact point both have equal slope, ray P R after reflection from circle too will pass from Q .
So, we have to find out a point R on circle such ray P R after reflection from circle will pass through Q .
Let point R be ( 5 0 cos θ , 5 0 sin θ )
Now, equation of tangent at R will be x cos θ + y sin θ = 5 0
Now, as P R after reflection from circle or tangent will pass from Q , mirror image of P about tangent is collinear with Q R . Let mirror image be P ′ ( a , b )
For mirror image of P about tangent,
cos θ a + 1 0 0 = sin θ b − 1 0 0 = − 2 cos 2 θ + sin 2 θ a cos θ + b sin θ − 5 0
( a , b ) = ( 2 0 0 cos 2 θ − 2 0 0 sin θ cos θ + 1 0 0 cos θ − 1 0 0 , − 2 0 0 sin 2 θ + 2 0 0 sin θ cos θ + 1 0 0 sin θ + 1 0 0 )
Now, as P ′ , Q , R are collinear
a − 5 0 cos θ b − 5 0 sin θ = 5 0 cos θ − 0 5 0 sin θ − 1 0 0
sin θ + 4 cos 2 θ − 4 sin θ cos θ + 2 cos θ − 2 = 0
3 2 cos 4 θ + 8 cos 3 θ − 2 7 cos 2 θ + 3 = 0
cos θ = − 1 , − 0 . 3 3 9 5 , 0 . 4 , 0 . 6 9
Now, we know from diagram and common sense that ellipse touches circle in 2 n d quadrant and that too not too down. So, cos θ = − 0 . 3 3 9 5 is only logical value. So, sin θ = 0 . 9 4 0 6
So, point R = ( − 1 6 . 9 7 5 , 4 7 . 0 3 ) .
So, length of path L = P R + R Q
L = 9 8 . 4 8 3 + 5 5 . 6 2 3
L = 1 5 4 . 0 9