Two Points On A Parabola
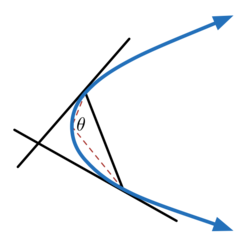 Two points are chosen at a parabola, such that tangents at these points are perpendicular to each other . Let the angle subtended by the chord joining the points at the vertex of the parabola be
θ
. Find the value of
θ
m
a
x
+
θ
m
i
n
in
degrees
.
Two points are chosen at a parabola, such that tangents at these points are perpendicular to each other . Let the angle subtended by the chord joining the points at the vertex of the parabola be
θ
. Find the value of
θ
m
a
x
+
θ
m
i
n
in
degrees
.
The answer is 216.87.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Sorry for the less detailed solution, I didn't have much time to write this..(its almost 1 A.M. in the morning and my mother is scolding me for sitting up late!)
I would like to know what's wrong with my approach.
I will work in parametric coordinates. The two points are clearly ( a t 2 , 2 a t ) and ( a / t 2 , − 2 a / t ) . ( I am working with the parabola y 2 = 4 a x ).
The angle between the lines made by joining the vertex to the above two points is given by:
tan θ = ∣ ∣ ∣ ∣ 1 − 4 2 / t + 2 t ∣ ∣ ∣ ∣ = 3 2 ∣ ∣ ∣ ∣ t + t 1 ∣ ∣ ∣ ∣
Finding the maximum and minimum value of the above expression doesn't give me the right answer. Where did I go wrong? :(
Log in to reply
Note that by using the formula which you used you can only obtain the acute angle between two lines. A better approach would be to use vectors in this case :)
Well, according to your approach, tan θ can never be negative. Why should that be the case? Since, tan θ being negative implies that θ > 9 0 o , which I think is possible.
I assume you have gone through the following approach:
Split θ into α , β (such that α is above the X-axis, and β is below the X-axis).
θ = α + β
Also,
tan α = a t 2 2 a t = t 2
tan β = t 2 a t − 2 a = − 2 t
I think you went wrong here. Maybe you assumed tan β to be positive (by taking the modulus)
@Anish Puthuraya and @Karthik Kannan , thank you both for your helpful replies. I think I see the error in my approach. As Karthik said, my formula does give the acute angle. The minimum acute angle from my formula comes out to be arctan ( 4 / 3 ) , this corresponds to maximum obtuse angle π − arctan ( 4 / 3 ) = 1 2 6 . 8 7 ∘ . This agrees with the given answer. Thank you once again.
Anish, it would be better to use ^{\circ} for the degree symbol. :)
The picture in the problem shows an angle not involving the parabola's vertex, which suggests (incorrectly) that as with a circle the angle made in this way is the same whichever point you choose.
I believe it's unnecessary to parameterise the parabola; it's sufficient to use y = x 2 to make life simpler. However, I'm past the time in my life when I want to do any significant amount of calculus. And I didn't know the geometry presented elsewhere here.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
|
Script result:
1 2 3 4 5 6 7 |
|
Fun question!
As a more convenient approach, we shall consider the parabola y 2 = 4 a x
It is a known fact that the tangents at the end points of the focal chord (the chord of the parabola which passes through its focus) intersect at 9 0 o to each other on the directrix of the parabola.
Hence, the two points chosen, must lie on the focal chord.
Also, the minimum angle subtended at the vertex by the end points of a focal chord is 9 0 o
To find the maximum angle subtended, we consider the focal chord which is drawn perpendicular to the axis of the parabola.
Therefore, the coordinates of the end points of the focal chord become : ( a , 2 a ) ; ( a , − 2 a )
The angle subtended by these two points at the vertex is : θ m a x = 2 tan − 1 2
θ m a x = 1 2 6 . 8 7 o
We already know that θ m i n = 9 0 o
Hence,
θ m a x + θ m i n = 1 2 6 . 8 7 o + 9 0 o = 2 1 6 . 8 7 o