Two-Prime Triples

We use the Euclid's formula for generating Pythagorean triples: $x,y,z$ is a Pythagorean triple if and only if $x = k(m^2-n^2), y = 2kmn, z = k(m^2+n^2)$ or $x = 2kmn, y = k(m^2-n^2), z = k(m^2+n^2)$ for some positive integers $k,m,n$ and $m > n$ . Because they are identical (we just swap $x$ and $y$ ), we will take the first formula ( $x = k(m^2-n^2), y = 2kmn, z = k(m^2+n^2)$ .

Note that if $k \neq 1$ , $z$ is not prime: $m^2+n^2 \ge 2^2 + 1^2 = 5 > 1$ , so $z$ can be factored to $k$ and $m^2+n^2$ , neither is equal to $1$ . $y$ is also not prime: $kmn \ge 2 \cdot 2 \cdot 1 = 4 > 1$ , so $y$ can be factored to $2$ and $kmn$ , neither is equal to $1$ . So at least two numbers are not prime and hence it's impossible for exactly two numbers to be prime (we only have three numbers, $x,y,z$ , to choose from). So $k = 1$ . This simplifies the formulas: $x = m^2 - n^2, y = 2mn, z = m^2 + n^2$ .

Now note that $y$ is still not prime: $mn \ge 2 \cdot 1 = 2 > 1$ , so $y$ can be factored to $2$ and $mn$ , neither is equal to $1$ . So we need both $x$ and $z$ to be prime.

Note that $x = m^2 - n^2 = (m+n)(m-n)$ . If $m-n > 1$ , then as $m+n \ge 2+1 = 3 > 1$ , $x$ can be factored to $m+n$ and $m-n$ , neither is equal to 1, so $x$ is not prime, contradicting our conclusion in the previous paragraph. So $m-n = 1$ . We substitute $m = n+1$ everywhere, giving further simplified formulas: $x = (n+1)^2 - n^2 = 2n+1$ , $y = 2(n+1)n$ , $z = (n+1)^2 + n^2 = 2n^2 + 2n + 1$ .

Note that $z \le 100 < 113$ . Substituting our formula above, $2n^2 + 2n + 1 < 113$ , or $2n^2 + 2n - 112 = 2(n^2 + n - 56) = 2(n+8)(n-7) \le 0$ . So $-8 < n < 7$ . Since $n \ge 1$ , we have $1 \le n < 7$ ; this gives six values of $n$ to check from (namely $1,2,3,4,5,6$ ).

We can check these six values manually by plugging to our simplified formulas:

• When $n = 1$ , $x = 3$ and $z = 5$ are primes.
• When $n = 2$ , $x = 5$ and $z = 13$ are primes.
• When $n = 3$ , $z = 25$ is not prime.
• When $n = 4$ , $x = 9$ is not prime.
• When $n = 5$ , $x = 11$ and $z = 61$ are primes.
• When $n = 6$ , $z = 85$ is not prime.

So the only valid choices for $z$ are $5,13,61$ , and hence their sum is $\boxed{79}$ .

x^2+y^2 = z^2 , Since two numbers of (x,y,z) are prime . Either of (x,y) are prime (or both are prime).
So lets assume in any case ‘ x’ is always prime. x^2= z^2-y^2. =>x^2= (z+y)(z-y) Case:I z+y= x , z-y=x => y=0 , therefore not possible Case:II z+y=x^2 , z-y=1. ( z+y=1, is not possible) z= y+1, z^2-y^2 = {y+1}^2 – y^2 x^2 = 2y+1 , x is prime , therefore substitute x = {2,3,5,7,11,13,17 etc } if ‘x’ exceeds 17 , y > 100 . Therefore substitute till 13 and check for either (y,z) is prime.
We get values of z as {5,13,61} Sum = 79.

We consider $x^2,y^2,z^2 (mod 3)$ . Each of $x^2,y^2,z^2 (mod 3)$ can only hold values 0 or 1, so at least one of $x^2$ or $y^2$ is 0 mod 3 (since 1+1=2 mod 3), and thus at least one of x and y is a multiple of 3.

Next we consider modulo 5. Each of $x^2,y^2,z^2$ modulo 5 can only hold values 0, 1 or 4, so we can deduce that at least one of $x^2, y^2, z^2$ must be 0 mod 5, and thus at least one of x,y,z is a multiple of 5.

Now we consider $x,y,z (mod 4)$ and $x^2, y^2, z^2 (mod 8)$ . $x^2, y^2, z^2$ can only take values of 0, 1 and 4. So we can deduce that at least one of x,y,z is 0 mod 8 and thus a multiple of 4.

Hence, we have at least a multiple of 3, 4 and 5 in x, y and z.

Case 1: One integer is a multiple of 4 (and not 3 or 5), the other 2 are prime.

In this case, the other 2 integers are obviously 3 and 5. By considering $3^2 + 5^2$ and $5^2 - 3^2$ it is easy to see that $(3,4,5)$ and $(4,3,5)$ are the only possible triples and $z=5$ .

Case 2: One integer is a multiple of 12 (and not 5), the other 2 are prime.

One of the integers must be 5. Since the composite integer is at least 12 (more than 5), 5 must be either x or y. Without loss of generalization let it be x. We can construct $5^2 = (z-y)(z+y)$ . Since y, z positive, we have $z-y=1$ and $z+y=25$ . Therefore $y=12$ and $z=13$ . We have two triples $(5,12,13)$ and $(12,5,13)$ with $z=13$ .

Case 3: One integer is a multiple of 20 (and not 3), the other 2 are prime.

One of them must be 3. Similar to case 2, we can construct $3^2 = (z-y)(z+y)$ with $z-y=1$ and $z+y=9$ . We get $y=4$ and $z=5$ , which will produce identical triples as case 1.

Case 4. One integer is a multiple of 60, the other 2 are prime.

Considering mod 3, we can deduce further that if both x and y are $0 mod 3$ then z is also $0 mod 3$ , and this will result in at least 2 composite integers. So only 1 of x and y is $0 mod 3$ , and thus z is $1 mod 3$ . So we can construct $60^2 + y^2 = z^2$ , so $y^2 = (z-60)(z+60)$ and so $z-60=1$ and $z+60=y^2$ . This will then produce the following 2 triples $(11,60,61)$ and $(60,11,61)$ .

Therefore, possible z-values are $5, 13, 61$ , giving us a total of $79$ .

Let the primitive triple be (x,y,z) where z is the hypoteneuse.We use the facts that for a primitive triple, 1.Exactly one of x,y,z is divisible by 3. 2.Exactly one of x,y is divisible by 4. 3.Exactly one of x,y,z is divisible by 5. 4.Exactly one of x,y is odd and z is always odd. So let x be the even number.We can immediately rule out x=2 as there is no triple having two as its member. Then according to our condition, y and z are primes. With result 3, It is safe to say that either z=5, y=5 or 5 divides x.We immediately get solutions for the first two cases, (3,4,5) and (12,5,13).From here we obtain 2 values of z, 5 and 13. Now we consider case 3- that 5 divides x. Now x could be 5, but that case has been taken care of.Then x is a multiple of 5.Also from argument 2 and 1, x is a multiple of 3 and 4 as well.Since 3,4,5 are relatively prime, their product divides x.So 60 divides x.But x is less than 100 since z is less than or equal to 100, x must be 60.Note that we need not consider z=4 and z=3 as the smallest possible value of z is 5.Coming back, we have x=60. This corresponds to z=61 and y=11.You may guess this or you may put x=60 in the pythagoras theorem, to get (z+60)(z-60)=y squared.Now we intend to get just one factor of the left hand side, so we put z-60=1 and hence z=61, which satisfies. So adding up the values of z, we obtain 61+13+5=79.

Any primitive Pythagorean triple (x,y,z) can be expressed in the form : [ (2mn) , (m^2 -n^2) , (m^2 + n^2) ], where m > n and m and n are positive integers. You may also express it in the form : [ (m^2 - n^2) , (2mn) , (m^2 + n^2) ]. Note that, always z= (m^2 + n^2). From the problem it is clear that we are only interested in primitive Pythagorean triples (x,y,z) , i.e. in which x, y and z are coprime. Now, (2mn) can not be prime. So both ( m^2 - n^2 ) and (m^2 + n^2) must be prime. Again, (m^2 - n^2) = (m + n)(m - n). So, for (m^2 - n^2) to be prime, (m - n)=1 and (m + n) must be prime. So we get the following ordered pairs (m,n) keeping z less than equal to 100 : (2,1) ; (3,2) ; (4,3) ; (6,5) and (7,6). Among them the ordered pairs (m,n) for which z = (m^2 + n^2) is prime are (2,1) ; (3,2) and (6,5). The corresponding values of z are (2^2 + 1^2) = 5 ; (3^2 + 2^2) = 13 and (6^2 + 5^2) = 61. Therefore the required sum = (5 + 13 + 61) = 79

Formulas for generating Pythagorean triples states that the integers

$x={{a}^{2}}-{{b}^{2}},\text{ }y=2ab,\text{ }z={{a}^{2}}+{{b}^{2}}$

form a Pythagorean triple. $a\ge2$ , $a>b$ . $y$ is even we must find x and z being prime.

$x=a^2-b^2=(a+b)(a-b)$

$a-b$ must be 1 or $a=b+1$

$z=a^2+b^2$

for $z\le100$ ,

$\begin{aligned} {{a}^{2}}+{{b}^{2}} & \le 100 \\ {{\left( b+1 \right)}^{2}}+{{b}^{2}} & \le 100 \\ {{b}^{2}}+2b+1+{{b}^{2}} & \le 100 \\ 2{{b}^{2}}+2b & \le 99 \\ 2b\left( b+1 \right) & \le 99 \\ b & \le 6 \end{aligned}$

or $a\le7$

for $a=2,3,4,5,6,7$ then

$x=3,5,7,9,11,13$

for $x=3,5,7,11,13$ then

$z=5,13,25,61,85$

$z$ which is prime are 5,13, and 61. 5 + 13 + 61 = 79

Clearly, one of the numbers $x,\ y,\ z$ must be even. Note that if this even number is a prime, it must be $2$ . Then $z=2$ does not work, so either $x=2$ or $y=2$ . Without loss of generality, assume $x=2$ . Then $4+y^2=z^2,$ which is impossible because for $y \geq 2$ we have $y^2 < 4+y^2 < y^2 + 2y +1$ , thus $y^2+4$ lies between two consecutive squares, so it is not a square. Therefore, the even number must be composite, and the other two numbers are odd primes. Note that $z$ cannot be even, because odd squares are $1$ modulo $4$ , so a sum of two odd squares cannot be divisible by $4$ . Thus, either $x$ or $y$ is even, and the other two numbers are prime. Without loss of generality, we can assume that $x$ is even. Then $y^2=z^2-x^2=(z-x)(z+x)$ . Because $y$ is prime and $1\leq z-x < z+x$ , this implies $z-x=1,\ y^2=z+x.$ Thus, we must have $x=2k,\ z=2k+1$ for some natural number $k\geq 2$ , and $4k+1=y^2$ . Note that $z\leq 100$ implies that $y^2\leq 199.$ Therefore $y$ must be one of the prime numbers $3,5,7,11,13$ . Note that $z=(y^2+1)/2$ is prime for $y= 3,\ 5$ and $11$ and composite for $y=7$ and $13.$ The corresponding values of $z$ are $5,\ 13,$ and $61,$ which add up to $79$ .

Every bit as bad as using a computer.

(Consider the power that would result from blending your mathematical and computing skills.)

take 3 variables a,b,c. take two other variables q,p.(p<q) start by taking p=1,q=2. a=q (square)-p(squared) b=2 p q c=q(squared)+p(squared) substitute,p,q in a,b,c by taking p=1,q=2, a=4-1=3 b=2*2=4 c=4+1=5 we get the pythagorean triples as (3,4,5) like this if we continue the highest triple having z below hundred will be(11,60,61) there will be three triples having atleast 2 primes, (3,4,5),(5,12,13) &(9,60,61) sum of all z values=5+13+61=79

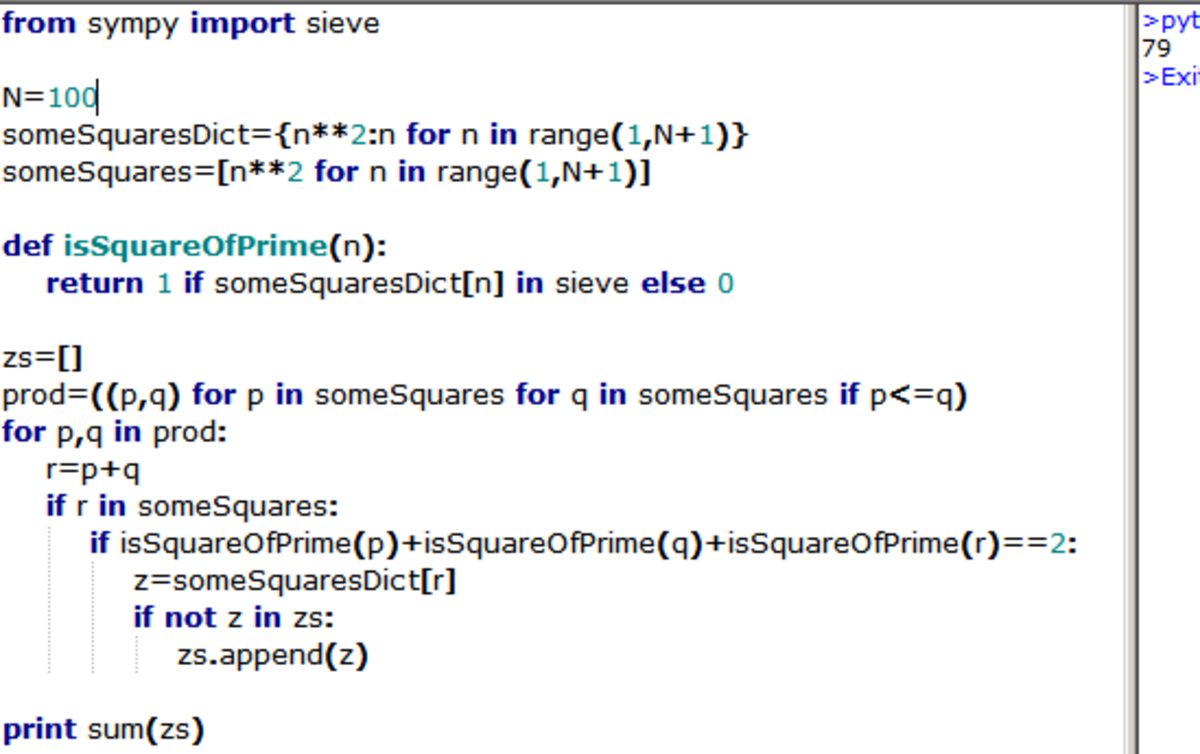
print sum([(z) for x in range(1,101) for y in range(1,101) for z in range(1,101) if x 2+y 2==z 2 and x>y and (p(x)+p(y)+p(z)==2)])**

Take a positive odd number k. $k^2$ can be represented as ${(k^2+1)^2}/4 - {(k^2-1)^2}/4$ So ${(k^2-1)^2}/4$ + $k^2$ = ${(k^2+1)^2}/4$ here z= ${(k^2+1)/2}$ , y =k , x= ${(k^2-1)/2}$ we will take y a prime. while y=3,5,11 then z will be respectively 5,13 and 61 and x will be respectively 4,12,60. Then the three pairs maintaing given conditions are $(4,3,5)$ , $(12,5,13)$ , $60,11,61)$ so the answer is 5+13+61 = 79

We can narrow down the possible values of $z$ using basic concepts.

There are no pythagorean triples where any of $x$ , $y$ , or $z$ are equal to 2. We can then direct our attention to odd primes. Also, at least one of $x$ or $y$ must be a prime, so we will allow $x$ to be prime.

The equation above could be written as

$x^2 = (z-y)(z+y)$ .

This yields $x^2 \equiv z^2 \pmod{y}$ , implying that $z$ is also odd. But if $y$ were the other odd prime, $z$ would be even (which it is not). So $z$ must be the other odd prime.

Because the factors of the right hand side of this can't both be equal to $x$ , and $z-y>z+y$ for positive integers $z$ and $y$ ,

$z-y=1$ and $z+y=x^2$ .

Thus, rearranging, we have the equation

$x^2=2z-1$

for prime $x$ and $z$ . So $z$ must be a prime of the form $\frac{x^2+1}{2}$ for prime $x$ . $z \le 100$ implies $x^2=2z-1 \le 199$ . The largest perfect square less than 199 is $169=13^2$ . Thus

$x \in \{3,5,7,11,13\}$ and $z \in \{5,13,25,61,85\}$ .

Restricting $z$ to be prime yields $z \in \{5,13,61\}$ .

$5+13+61 = \boxed{79}$

Java code:

public class Pyth {
    public static void main(String[] args){
        int prime[] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,49,53,59,61,67,71,73,79,83,89,97};
        for(int z=5;z<=100;z++){
            for(int x=2;x<z;x++){
                int y = ((int)(Math.sqrt(z*z-x*x)));
                if(y*y==z*z-x*x){
                    int primeCount = 0;
                    for(int i=0;i<prime.length;i++)
                        if(prime[i]==x||prime[i]==y||prime[i]==z)
                            primeCount++;
                    if(primeCount==2)
                        System.out.println(x+" "+y+" "+z);
                }
            }
        }
    }
}

Output:

3 4 5
4 3 5
5 12 13
12 5 13
11 60 61
60 11 61

the list of Pythagorean Triples with z<=100 are: ( 3, 4, 5 ) ( 5, 12, 13) ( 8, 15, 17) ( 7, 24, 25) (20, 21, 29) (12, 35, 37) ( 9, 40, 41) (28, 45, 53) (11, 60, 61) (16, 63, 65) (33, 56, 65) (48, 55, 73) (13, 84, 85) (36, 77, 85) (39, 80, 89) (65, 72, 97). according to the terms, 2 of the numbers must be prime number, and the sets of Pythagorean Triples which have that such terms are ( 3, 4, 5 ) ( 5, 12, 13) and (11, 60, 61), so the sum of each z is 5+13+61 = 79

Here is a list of all the Primitive Pythagorean Triples with z ≤ 100

3, 4, 5; 5, 12, 13; 8, 15, 17; 7, 24, 25; 20, 21, 29; 12, 35, 37; 9, 40, 41; 28, 45, 53; 11, 60, 61; 33, 56, 65; 16, 63, 65; 48, 55, 73; 13, 84, 85; 36, 77, 85; 39, 80, 89; 65, 72, 97

Out of this list, only three triples have exactly two of the numbers x, y, and z bring prime. They are 3, 4, 5; 5, 12, 13; and 11, 60, 61. Hence, you add all three z's together, 5, 13, and 61, to get your answer-79.