Two Rectangles on a Quarter Circle
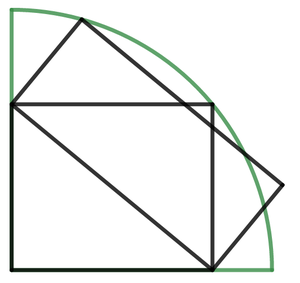
A rectangle is inscribed within a quarter circle of radius 6 cm . Another rectangle is constructed on the diagonal of the first, with one of its corners on the quarter circle, like in the diagram above.
If the two rectangles had equal areas, what would that area be, in cm 2 ?
The answer is 16.9705627485.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Very nice solution. I noticed also that if the rectangles had equal areas, the corner of the inscribed rectangle (on the circle) would be on the side of the second rectangle. I haven't tried, but perhaps knowing this would make the problem easier.
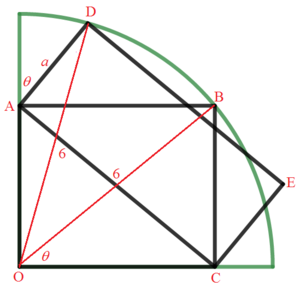
As labelled in the figure, we note that the area of the rectangle A B C O , A = O B ⋅ B C = 3 6 sin θ cos θ and the area of rectangle A D E C , A C ⋅ A D = 6 a . Therefore, a = 6 sin θ cos θ .
Applying cosine rule on △ O A D , we have:
O D 2 6 2 3 6 3 6 1 = A D 2 + A O 2 − 2 A D ⋅ A O cos ∠ O A D = a 2 + ( 6 sin θ ) 2 − 2 a ( 6 sin θ ) cos ( 1 8 0 ∘ − θ ) = a 2 + 3 6 sin 2 θ + 1 2 a sin θ cos θ = 1 0 8 sin 2 θ cos 2 θ + 3 6 sin 2 θ = 3 sin 2 θ cos 2 θ + sin 2 θ Note that cos ( 1 8 0 ∘ − θ ) = − cos θ Recall a = 6 sin θ cos θ
⟹ 3 sin 4 θ − 4 sin 2 θ + 1 ( 3 sin 2 θ − 1 ) ( sin 2 θ − 1 ) = 0 = 0
⟹ sin θ = 3 1 , since θ < 9 0 ∘ and cos θ = 1 − 3 1 = 3 2 and the area A = 3 6 sin θ cos θ = 1 2 2 ≈ 1 6 . 9 7 1 .
.... with side lengths ( 2 6 , 2 3 ) and ( 6 , 2 2 ) , respectively. I used the cosine rule, Pythagoras and a bit of algebra. Did you find an elegant geometric approach?
Log in to reply
With the given quarter circle of radius 6 cm, there's only one variable, which I've selected that point on the y-axis to be. From that, we find the distance from that point to the quarter circle, which then sets up the equation to be solved. From that, find area. I don't think it's elegant but does get the job done.
Let the vertex of the inscribed rectangle be ( 6 cos t , 6 sin t ) , (Note that t is the angle that the diagonal connecting the origin to that vertex, makes with the horizontal axis), then
Area = 3 6 sin t cos t
Point p , where the second rectangle touches the quarter circle, is given by
p = ( 0 , 6 sin t ) + c ( sin t , cos t )
where c is yet to be determined. Substituting the coordinates of this point into x 2 + y 2 = 3 6 , yields
c 2 + 6 c sin 2 t − 1 8 − 1 8 cos 2 t = 0 ( 1 )
Now, the condition on the areas of the two rectangles, implies,
6 c = 3 6 sin t cos t
Hence, c = 6 sin t cos t = 3 sin 2 t
Substituting this last equation into Eq. (1) , yields,
9 sin 2 2 t + 1 8 sin 2 2 t − 1 8 − 1 8 cos 2 t = 0
so that
3 sin 2 2 t − 2 − 2 cos 2 t = 0
Define u = 2 t , then this becomes,
3 ( 1 − cos 2 u ) − 2 − 2 cos u = 0
Re-arranged,
3 cos 2 u + 2 cos u − 1 = 0
And finally,
( 3 cos u − 1 ) ( cos u + 1 ) = 0
cos u = 1 / 3
So that,
t = 2 1 cos − 1 ( 3 1 )
Remember, the area = 6 c = 1 8 sin 2 t
We know that cos 2 t = 3 1 , so sin 2 t = 3 8 , from which the area = 6 8 = 1 2 2 = 1 6 . 9 7 0 5 6 2 7 4 8 4 7 7 1 4