Two rings
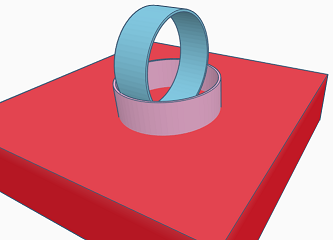
Two identical rings made of thin cardboard. One lays flat on a table and the other stands inside it. They touch at four points.
If the inner ring just touches the table, give the rings' ratio of diameter to width.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Thanks. My own solution was so cumbersome I didn't bother sharing. This was inspired by wrapping presents. Think spools of ribbon.
The picture on the left shows a side view of the two rings, and the picture on the right shows the top view.
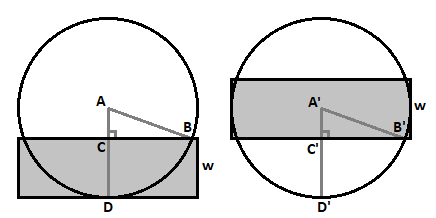
Let r be the radius of one ring and w be the width of one ring. Since r = A B = A ′ B ′ , B C = B ′ C ′ , and ∠ C = ∠ C ′ , △ A B C ≅ △ A ′ B ′ C ′ by hypotenuse-leg theorem, which means A C = r − w = A ′ C ′ . Therefore, 2 ( r − w ) = w , or 2 r = 3 w .
The ratio of the diameter to the width is then w 2 r = w 3 w = 3 .
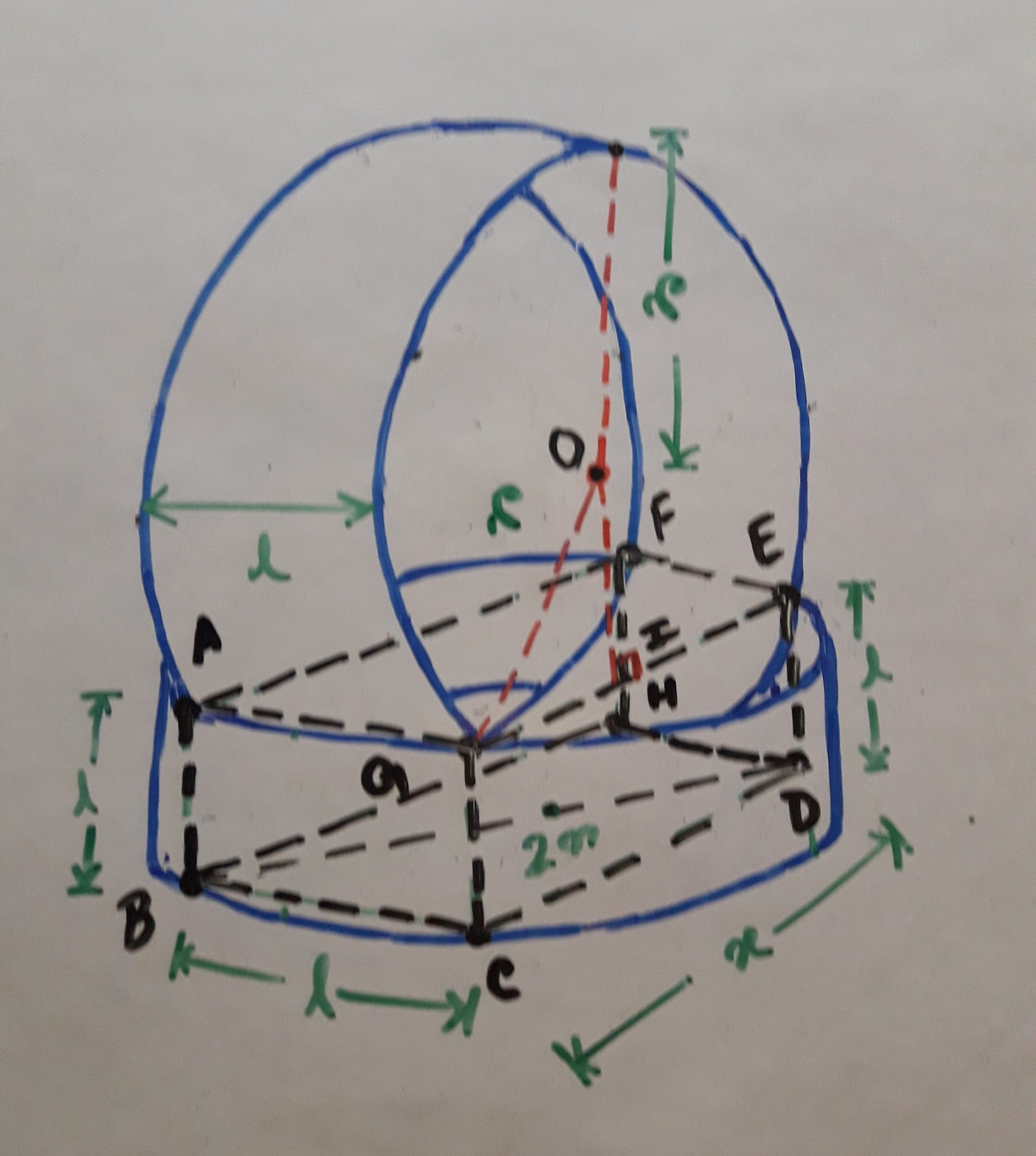

Let's say that the two rings are given by x 2 + y 2 = 1 and x 2 + z 2 = 1 ; at the points of intersection we have y 2 = z 2 . If the width of the rings is a , then the coordinates of the points of contact are y = ± 2 a and z = a − 1 . It is required that 4 a 2 = ( a − 1 ) 2 , with the smaller solution a = 3 2 . The ratio we seek is a 2 = 3 .
A nice problem, charming and playful!