Two semicircles and a small circle.
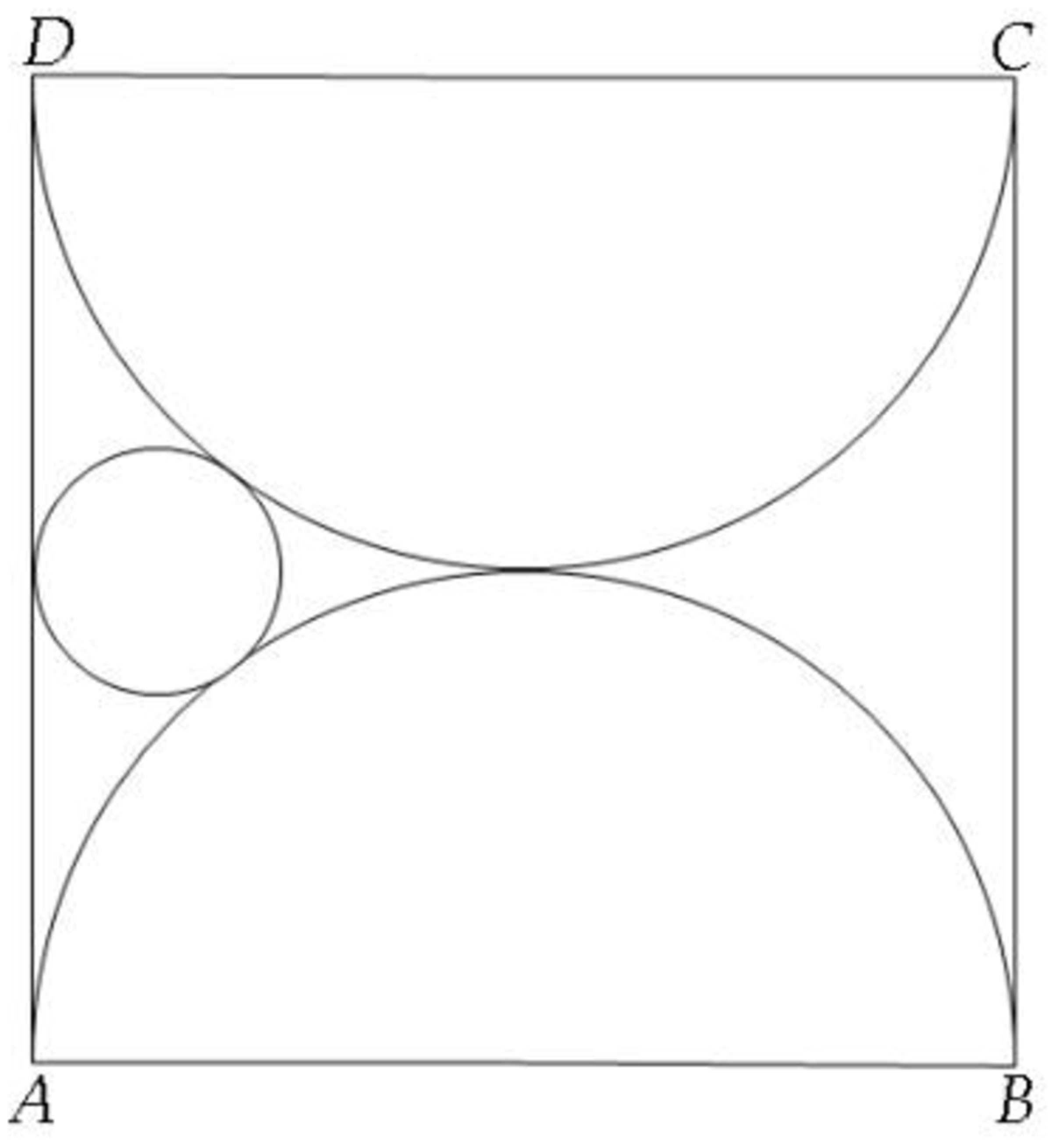Given a square
A
B
C
D
, there are two semicircles that are congruent. The two semicircles are each diameter on the sides of the
A
B
C
D
square. A small circle is placed in such a way as to offend two semicircular arcs and square upright sides. Determine the result if the length of the semicircle radius is divided by the length of the small circle radius.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
(
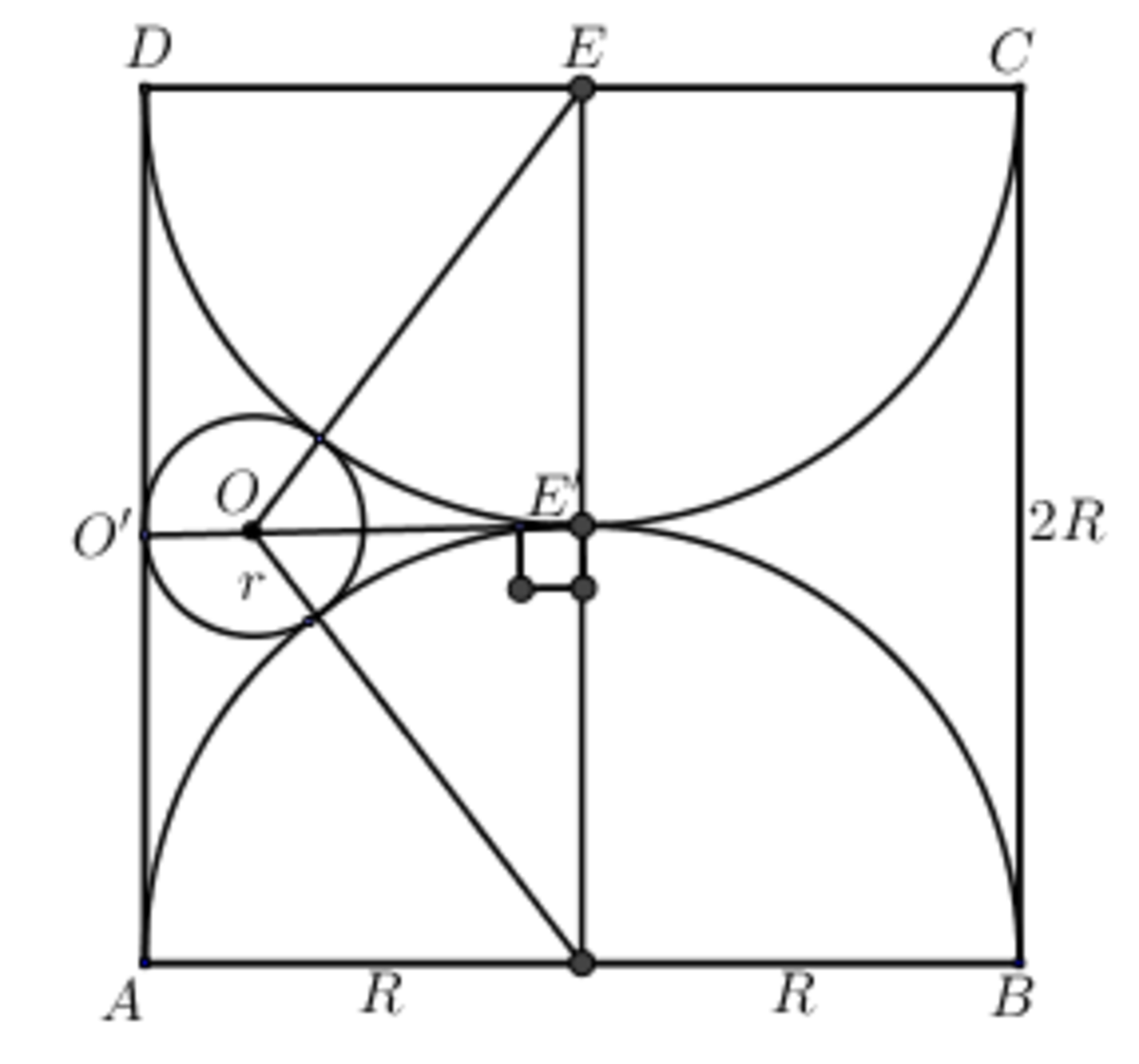O
E
′
)
2
=
O
E
2
−
(
E
E
′
)
2
(
O
′
E
′
−
O
′
O
)
2
=
(
R
+
r
)
2
−
R
2
(
R
−
r
)
2
=
(
R
+
r
+
R
)
(
R
+
r
−
R
)
R
2
+
r
2
−
2
R
r
=
(
2
R
+
r
)
r
R
2
+
r
2
−
2
R
r
=
2
R
r
+
r
2
R
2
=
4
R
r
R
=
4
r
r
R
=
4