Two similar equilateral triangles in a circle
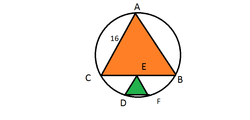 Two equilateral triangles reside in a circle, one on top of the other as shown in the figure above.
Two equilateral triangles reside in a circle, one on top of the other as shown in the figure above.
If E is the midpoint of the side B C of the larger orange triangle which has a side length of 1 6 and side D E of the smaller triangle is parallel to A C , find the length of D E correct to 2 decimal places.
The answer is 4.94.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
An elegant approach, Vijay. My approach was a slight variation on Niranjan's ...
Let O be the center of the circle, and focus on Δ O D E . Now O D is a radius of the circle, which is 3 2 the altitude of Δ A B C , i.e., ∣ O D ∣ = 3 2 ( 8 3 ) = 3 1 6 3 .
We also have that ∣ O E ∣ = 2 1 ∣ O D ∣ = 3 8 3 and ∠ O E D = 1 5 0 ∘ .
Then with ∣ D E ∣ = x , by the Cosine rule we see that
( 3 1 6 3 ) 2 = x 2 + ( 3 8 3 ) 2 − 2 x ( 3 8 3 ) cos ( 1 5 0 ∘ ) ⟹ x 2 + 8 x − 6 4 = 0
⟹ x = 2 − 8 ± 6 4 + 4 ∗ 6 4 = − 4 ± 4 5 ⟹ x = 4 ( 5 − 1 ) since x > 0 .
Nice approach. Up voted.The common approach would be as under.
Let O be the center of the circumcircle. R its radius. S=ED. M midpoint of DF.
R
2
=
(
O
E
+
E
M
)
2
+
D
M
2
,
∴
(
3
1
6
)
2
=
{
3
8
+
2
3
∗
S
}
2
+
(
2
S
)
2
∴
3
2
5
6
=
3
6
4
+
4
3
∗
S
2
+
2
∗
3
8
∗
2
3
∗
S
+
4
S
2
⟹
S
2
+
8
∗
S
−
6
4
=
0
S
o
l
v
i
n
g
f
o
r
S
>
0
,
S
=
4
.
9
4
4
Missed it due to calculation error.
Let the length of D E = x
Construction:
Extend the side D E to intersect the side A B of the triangle at G and the circle at H . Then since DG is parallel to A C , E G = 8 and G H = x by symmetry.
Using the properties of chords.
D E ⋅ E H = C E ⋅ E B
x ( 8 + x ) = 8 ⋅ 8
x 2 + 8 x = 6 4
Completing the square on the left, ( x + 4 ) 2 = 8 0 = 1 6 ⋅ 5
x = 4 ( 5 − 1 ) = 4 . 9 4